
分析 (1)先求出f(x)=$\frac{1}{2}×{2}^{x}$+$\frac{1}{2}$,由此能求出y=f(x)的反函数y=f-1(x)的解析式.
(2)推导出$F(x)={f^{-1}}({{2^{x-1}}})-{log_{\frac{1}{2}}}f(x)$=$lo{g}_{2}({2}^{x}-1)$-$lo{g}_{\frac{1}{2}}(\frac{{2}^{x}+1}{2})$,由F(x)≤0,得$lo{g}_{2}({2}^{x}-1)$≤$lo{g}_{\frac{1}{2}}(\frac{{2}^{x}+1}{2})$=$lo{g}_{2}(\frac{2}{{2}^{x}+1})$,由此能求出x取值范围.
解答 解:(1)∵f(x)=a•2x+b的图象过点$A({1,\frac{3}{2}})$,$B({2,\frac{5}{2}})$,
∴$\left\{\begin{array}{l}{2a+b=\frac{3}{2}}\\{4a+b=\frac{5}{2}}\end{array}\right.$,解得a=$\frac{1}{2}$,b=$\frac{1}{2}$,
∴f(x)=$\frac{1}{2}×{2}^{x}$+$\frac{1}{2}$,
设y=$f(x)=\frac{1}{2}×{2}^{x}+\frac{1}{2}$,
则2x=2y-1,x=log2(2y-1),
x,y互换得y=f(x)的反函数y=f-1(x)的解析式为y=f-1(x)=log2(2x-1),x$>\frac{1}{2}$.
(2)∵$F(x)={f^{-1}}({{2^{x-1}}})-{log_{\frac{1}{2}}}f(x)$
=$lo{g}_{2}(2×{2}^{x-1}-1)$-$lo{g}_{\frac{1}{2}}(\frac{1}{2}×{2}^{x}+\frac{1}{2})$=$lo{g}_{2}({2}^{x}-1)$-$lo{g}_{\frac{1}{2}}(\frac{{2}^{x}+1}{2})$,
F(x)≤0,
∴$lo{g}_{2}({2}^{x}-1)$≤$lo{g}_{\frac{1}{2}}(\frac{{2}^{x}+1}{2})$=$lo{g}_{2}(\frac{2}{{2}^{x}+1})$,
∴$\left\{\begin{array}{l}{{2}^{x}-1>0}\\{\frac{2}{{2}^{x}+1}>0}\\{{2}^{x}-1≤\frac{2}{{2}^{x}+1}}\end{array}\right.$,解得0<x<$lo{g}_{2}\sqrt{3}$.
∴x取值范围是(0,$lo{g}_{2}\sqrt{3}$).
点评 本题考查反函数的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意反函数、对数性质的合理运用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{25}{8}$ | C. | $\frac{23}{7}$ | D. | $\frac{157}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
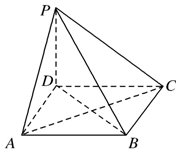 如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.
如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N={(-1,1)} | B. | M∩N=∅ | C. | M⊆N | D. | N⊆M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{7\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $-\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com