
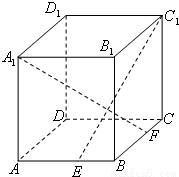
如图,ABCD-A1B1C1D1是正方体,E、F分别是AD、DD1的中点,则面EFC1B和面BCC1所成二面角的正切值等于
C
为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。
从图形特点看,应当过E(或F)作面BCC1的垂线.过E作EH⊥BC,垂足为H. 过H作HG⊥BC1,垂足为G.连EG.
∵面ABCD⊥面BCC1,而EH⊥BC
∵EH⊥面BEC1,
EG是面BCC1的斜线,HG是斜线EG在面BCC1内的射影.
∵HG⊥BC1, 
∴EG⊥BC1,
∴∠EGH是二面角E-BC1-C的平面角。
在Rt△BCC1中:sin∠C1BC=![]() =
=![]()
在Rt△BHG中:sin∠C1BC=![]()
∴HG=![]() (设底面边长为1).
(设底面边长为1).
而EH=1,
在Rt△EHG中:tg∠EGH=![]()
∴∠EGH=arctg![]()
故二面角E-BC1-C 等于arctg![]() .
. 


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
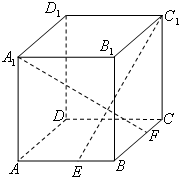 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是查看答案和解析>>
科目:高中数学 来源: 题型:

A.A、M、O三点共线 B.A、M、O、A1四点共面
C.A、O、C、M四点共面 D.B、B1、O、M四点共面
查看答案和解析>>
科目:高中数学 来源:2011年广东省江门市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com