
���� ������ȥ���������ɰ�C1��C2��Ϊ��ͨ���̣���$��=\frac{��}{2}$ʱ��P��Q�غϣ�������a��b��ֵ��
����ֱ��l��$\left\{{\begin{array}{l}{x=1-\frac{{\sqrt{2}}}{2}t}\\{y=-1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��tΪ��������C2�����������ҳ���ʽֱ�����|AB|��
��� �⣺����C1��x2+y2=1��C2��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
����=0ʱ��P��1��0����Q��a��0����|PQ|=a-1=2��a=3
��$��=\frac{��}{2}$ʱ��P��Q�غϣ�
��b=1��C2��$\frac{x^2}{9}+{y^2}=1$������5�֣�
����$\left\{{\begin{array}{l}{x=1-\frac{{\sqrt{2}}}{2}t}\\{y=-1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$����$\frac{x^2}{9}+{y^2}=1$�� $5{t^2}-10\sqrt{2}t+1=0$
��${t_1}+{t_2}=2\sqrt{2}$��${t_1}{t_2}=\frac{1}{5}$
��|AB|=$|{t_1}-{t_2}|=\sqrt{{{��{t_1}+{t_2}��}^2}-4{t_1}{t_2}}=\frac{{6\sqrt{5}}}{5}$����10�֣�
���� ���⿼�����������ŵĻ������������̵ļ������壬�������������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
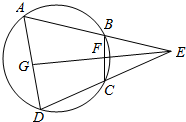 ��ͼ����֪�ı���ABCD�ڽ���Բ���ӳ�AB��DC����E��EGƽ�֡�E������BC��AD���ཻ��F��G����֤����CFG=��DGF��
��ͼ����֪�ı���ABCD�ڽ���Բ���ӳ�AB��DC����E��EGƽ�֡�E������BC��AD���ཻ��F��G����֤����CFG=��DGF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
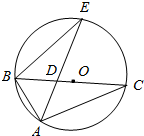 ��ͼ����ABC�ڽ���ԲO��AEƽ�֡�BAC��BC�ڵ�D������BE��
��ͼ����ABC�ڽ���ԲO��AEƽ�֡�BAC��BC�ڵ�D������BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
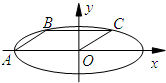 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ij��᳤Ϊ6����AΪ�㣬B��C����ԲE�ϣ����ı���OABCλƽ���ı��Σ��ҡ�OAB=30�㣮
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ij��᳤Ϊ6����AΪ�㣬B��C����ԲE�ϣ����ı���OABCλƽ���ı��Σ��ҡ�OAB=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
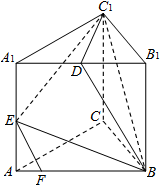 ��������ABC-A1B1C1�У�AB=BC=CA=AA1=2������AA1��ƽ��ABC��DΪ��A1B1���е㣬EΪAA1���е㣬��F����AB�ϣ���AF=$\frac{1}{4}$AB��
��������ABC-A1B1C1�У�AB=BC=CA=AA1=2������AA1��ƽ��ABC��DΪ��A1B1���е㣬EΪAA1���е㣬��F����AB�ϣ���AF=$\frac{1}{4}$AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com