
����Ŀ��ij�������Ž������ʵ������![]() �����Ⱥ�����ȡn�˽�����һ���Ƿ�ͨ�������ĵ��飬����ͨ�������ij�Ϊ��ʱ���塱�������Ϊ����ʱ���塱��ͨ������ֱ�õ���ͼ��ʾͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�����Ⱥ�����ȡn�˽�����һ���Ƿ�ͨ�������ĵ��飬����ͨ�������ij�Ϊ��ʱ���塱�������Ϊ����ʱ���塱��ͨ������ֱ�õ���ͼ��ʾͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��

����������⣺
����ȫƵ�ʷֲ�ֱ��ͼ����![]() ��ֵ��
��ֵ��
����![]() ������εġ�ʱ���塱�в��÷ֲ��������ȡ
������εġ�ʱ���塱�в��÷ֲ��������ȡ![]() �˲μ�����ʱ�д��˴���������ѡȡ
�˲μ�����ʱ�д��˴���������ѡȡ![]() ����Ϊ��ӣ���ѡȡ��
����Ϊ��ӣ���ѡȡ��![]() �������������
�������������![]() �������Ϊ
�������Ϊ![]() ����
����![]() �ķֲ���
�ķֲ���
���𰸡���Ƶ�ʷֲ�ͼ�ԣ�![]() ��
��![]() ��
��![]() ���Ƽ�����
���Ƽ�����
��������
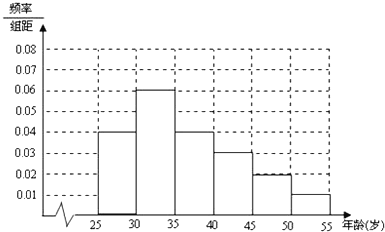
������������ε������Ϊ1����ڶ����Ƶ�ʣ�Ȼ������ߣ�����Ƶ��ֱ��ͼ�������һ���������Ƶ�ʴӶ����n�������֪���ڶ����Ƶ���Լ��������Ӷ����p��ֵ��Ȼ������������Ƶ�ʺ������Ӷ����a��ֵ��
������Ϊ[40��45��������εġ�ʱ���塱��[45��50��������εġ�ʱ���塱�ı�ֵΪ2��1�����Բ��÷ֲ��������ȡ18�ˣ�[40��45��������12�ˣ�[45��50��������6�ˣ�������X���ӳ����ηֲ���X��ȡֵ����Ϊ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��г��ֲ��У�
���ڶ����Ƶ��Ϊ![]() ��
��
���Ը�Ϊ![]() ��Ƶ��ֱ��ͼ���£�
��Ƶ��ֱ��ͼ���£�
��һ�������Ϊ![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ������
������![]()
�����֪���ڶ����Ƶ��Ϊ![]() �����Եڶ��������Ϊ
�����Եڶ��������Ϊ![]() ��
��
����![]() ��
��
�������Ƶ��Ϊ![]() �����Ե����������Ϊ
�����Ե����������Ϊ![]() ��
��
����![]()
����Ϊ[40��45��������εġ�ʱ���塱��[45��50��������εġ�ʱ���塱�ı�ֵ
Ϊ![]() ��
��
���Բ��÷ֲ��������ȡ18�ˣ�[40��45��������12�ˣ�[45��50��������6�ˣ�
�������![]() ���ӳ����ηֲ�
���ӳ����ηֲ�
![]() ��
��![]() ��
��![]()
![]() ,
,
�����������X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һλ���۾����ռ�����ÿ�����۶�y(ǧԪ)�����۾���x(��)�Ĺ�ϵ��
���۾���x/�� | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
�����۶�y/ǧԪ | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)������Щ���ݻ���ɢ��ͼ����ֱ��![]() ��78��4.2x������
��78��4.2x������![]() ��
��
(2)������Щ������ع�ֱ�߷��̲��ݴ˼���![]() ��
��
(3)�Ƚ�(1) (2)�еIJв�ƽ����![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ���
��б��![]() ����ͨ��
����ͨ��![]() ��ֱ��
��ֱ��![]() Ϊ����ת�õ����Ҷ����
Ϊ����ת�õ����Ҷ����![]() ��ֱ����ǣ�����
��ֱ����ǣ�����![]() ��б��
���![]() ��.
��.
��1����DΪAB���е�ʱ��������ֱ��AO��CD���ɽǵ�����ֵ��
��2����CD��ƽ��AOB���ɽǵ�����ֵ�����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5����Ʒ�У���3��һ��Ʒ��2������Ʒ��������ȡ2������![]() Ϊ���ʵ��¼���(����)
Ϊ���ʵ��¼���(����)
A. ǡ��1��һ��Ʒ B. ������һ��һ��Ʒ
C. ������һ��һ��Ʒ D. ������һ��Ʒ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A������1�������1������B������2�������1������A������ȡ1������B������ȡ1�����������Ļ���������һ�Σ���
(1)A���к���ǡ��1���ĸ��ʣ�
(2)A���к���������1���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A.B���ֹ��IJ�Ʒ����Ȣ�ڼס�����̨�����ϸ��ӹ�һ��������ܳ�Ϊ��Ʒ����֪A��Ʒ��Ҫ�ڼ����ϼӹ�3Сʱ�����һ����ϼӹ�1Сʱ��B��Ʒ��Ҫ�ڼ����ϼӹ�1Сʱ�����һ����ϼӹ�3Сʱ����һ���������ڣ���������ֻ��ʹ��11Сʱ���һ�������ֻ��ʹ��9Сʱ��A��Ʒÿ������300Ԫ��B��Ʒÿ������400Ԫ��������̨������һ���������ڴ�������������___________Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|2x��1|+|x+1|��
��1������f��x����ֵ��M��
��2����a��M���ԱȽ�|a��1|+|a+1|�� ![]() ��
�� ![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC�ڽ�A��B��C�ĶԱߣ� ![]() ��
��
�������B�Ĵ�С��
��������ABC��AC�ϵĸ�h=b���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x2+bln��x+1����[0��+�ޣ��ϵ����ݼ�����b��ȡֵ��Χ�� ��
A.[0��+�ޣ�
B.[�� ![]() ��+�ޣ�
��+�ޣ�
C.�����ޣ�0]
D.�����ޣ��� ![]() ]
]
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com