
【题目】已知函数f(x)=|x﹣1|﹣2|x+1|的最大值为k.
(1)求k的值;
(2)若a,b,c∈R, ![]() ,求b(a+c)的最大值.
,求b(a+c)的最大值.
【答案】
(1)解:由于f(x)= 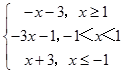 ,
,
当x≥﹣1时,f(x)max=f(1)=1﹣3=﹣4,
当﹣1<x<1时,f(x)<f(﹣1)=3﹣1=2,
当x≤﹣1时,f(x)max=f(﹣1)=﹣1+3=2,
所以k=f(x)max=f(﹣1)=2
(2)解:由已知 ![]() ,有(a2+b2)+(b2+c2)=4,
,有(a2+b2)+(b2+c2)=4,
因为a2+b2≥2ab(当a=b取等号),b2+c2≥2bc(当b=c取等号),
所以(a2+b2)+(b2+c2)=4≥2(ab+bc),即ab+bc≤2,
故[b(a+c)]max=2
【解析】(1)根据分段函数的单调性求出函数的最大值,即可求出k的值,(2)根据基本不等式即可求出答案
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1﹣m)lnx+ ![]() ﹣x,m∈R且m≠0.
﹣x,m∈R且m≠0.
(Ⅰ)当m=2时,令g(x)=f(x)+log2(3k﹣1),k为常数,求函数y=g(x)的零点的个数;
(Ⅱ)若不等式f(x)>1﹣ ![]() 在x∈[1,+∞)上恒成立,求实数m的取值范围.
在x∈[1,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中组织数学知识竞赛,采取答题闯关的形式,分两种题型,每种题型设两关.“数学文化”题答对一道得5分,“数学应用”题答对一道得10分,答对一道题即可进入下一关,否则终止比赛.有甲、乙、丙三人前来参赛,设三人答对每道题的概率分别是 ![]() 、
、 ![]() 、
、 ![]() ,三人答题互不影响.甲、乙选择“数学文化”题,丙选择“数学应用”题.
,三人答题互不影响.甲、乙选择“数学文化”题,丙选择“数学应用”题.
(Ⅰ)求乙、丙两人所得分数相等的概率;
(Ⅱ)设甲、丙两人所得分数之和为随机变量X,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”. 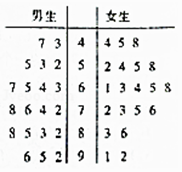
(1)完成下面2×2列联表,
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(2)判断是否有90%的把握认为“空间想象能力突出”与性别有关;
(3)从“空间想象能力突出”的同学中随机选取男生2名、女生2名,记其中成绩超过90分的人数为ξ,求随机变量ξ的分布列和数学期望. 下面公式及临界值表仅供参考: ![]()
P(X2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是 ①对于命题p:x∈R,使得x2+x+1<0,则p:x∈R,均有x2+x+1>0;
②命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
③设ξ~B(n,p),已知Eξ=3,Dξ= ![]() ,则n与p值分别为12,
,则n与p值分别为12, ![]()
④m=3是直线(m+3)x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件.( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有10人.在20名女性驾驶员中,平均车速超过100km/h的有5人,不超过100km/h的有15人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关;
平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 | |||
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过100km/h的车辆数为ζ,若每次抽取的结果是相互独立的,求ζ的分布列和数学期望.
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知椭圆 ![]() 的左焦点为F,离心率为
的左焦点为F,离心率为 ![]() ,过点F且垂直于长轴的弦长为
,过点F且垂直于长轴的弦长为 ![]() .
.
(I)求椭圆C的标准方程;
(Ⅱ)设点A,B分别是椭圆的左、右顶点,若过点P(﹣2,0)的直线与椭圆相交于不同两点M,N.
(i)求证:∠AFM=∠BFN;
(ii)求△MNF面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com