
【题目】已知函数f(x)=x|x+a|﹣ ![]() lnx.
lnx.
(1)当a=0时,讨论函数f(x)的单调性;
(2)若a<0,讨论函数f(x)的极值点.
【答案】
(1)解:当a=0时,f(x)=x2﹣ ![]() lnx,函数的定义域为(0,+∞).
lnx,函数的定义域为(0,+∞).
f′(x)= ![]() ,
,
令f′(x)>0,可得x> ![]() ,f′(x)>0,可得0<x<
,f′(x)>0,可得0<x< ![]() ,
,
∴函数f(x)的单调增区间是( ![]() ,+∞),单调减区间是(0,
,+∞),单调减区间是(0, ![]() )
)
(2)解:当a<0时,f(x)= 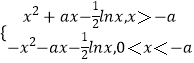 .
.
①x>﹣a时,f′(x)= ![]() =0,可得x1=
=0,可得x1= ![]() ,x2=
,x2= ![]() <﹣a(舍去).
<﹣a(舍去).
若 ![]() ≤﹣a,即a≤﹣
≤﹣a,即a≤﹣ ![]() ,f′(x)≥0,∴函数f(x)在(﹣a,+∞)上单调递增;
,f′(x)≥0,∴函数f(x)在(﹣a,+∞)上单调递增;
若 ![]() >﹣a,即﹣
>﹣a,即﹣ ![]() <a<0,则当x∈(﹣a,x1)时,f′(x)<0,x∈(x1,+∞),f′(x)>0,
<a<0,则当x∈(﹣a,x1)时,f′(x)<0,x∈(x1,+∞),f′(x)>0,
∴f(x)在∈(﹣a,x1)上单调递减,在(x1,+∞)上单调递增.
②当0<x<﹣a时,f′(x)= ![]() =0,得﹣4x2﹣2ax﹣1=0.
=0,得﹣4x2﹣2ax﹣1=0.
记△=4a2﹣16.
△≤0,即﹣2≤a<0,f′(x)≤0,∴f(x)在(0,﹣a)上单调递减;
△>0,即a<﹣2,f′(x)=0可得x3= ![]() ,x4=
,x4= ![]() 且0<x3<x4<﹣a.
且0<x3<x4<﹣a.
x∈(0,x3)时,f′(x)<0,x∈(x3,x4)时,f′(x)>0,x∈(x4,﹣a),f′(x)<0,
∴f(x)在(0,x3)上单调递减,在(x3,x4)上单调递增,在(x4,﹣a)上单调递减,
综上所述,a<﹣2时,f(x)的极小值点为 ![]() ,极大值点为
,极大值点为 ![]() ;﹣2≤a≤﹣
;﹣2≤a≤﹣ ![]() 时,f(x)无极值点;
时,f(x)无极值点;
﹣ ![]() <a<0时,f(x)的极小值点为
<a<0时,f(x)的极小值点为 ![]()
【解析】(1)当a=0时,f(x)=x2﹣ ![]() lnx,函数的定义域为(0,+∞),求导数,断导数的符号,即可判断f(x)的单调性;(2)分类讨论,利用极值的定义,即可讨论函数f(x)的极值点.
lnx,函数的定义域为(0,+∞),求导数,断导数的符号,即可判断f(x)的单调性;(2)分类讨论,利用极值的定义,即可讨论函数f(x)的极值点.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值与导数(求函数
在这个区间单调递减),还要掌握函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值)的相关知识才是答题的关键.
是极小值)的相关知识才是答题的关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
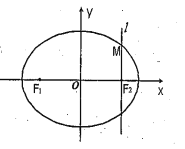
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]()
![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2>已知![]() 经过点
经过点![]() 且斜率为
且斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]()
(1)若![]() 且函数
且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下, 当![]() 时,
时, ![]() 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设![]() ,
, ![]()
![]() 且
且![]() 为偶函数, 判断
为偶函数, 判断![]() +
+![]() 能否大于零?请说明理由.
能否大于零?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 是双曲线
是双曲线![]() 的左,右焦点,点
的左,右焦点,点![]() 在双曲线上,且
在双曲线上,且![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
B. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
C. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
D. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合P={(x,y)||x|+|y|≤1,x∈R,y∈R},Q={(x,y)|x2+y2≤1,x∈R,y∈R},R={(x,y)|x4+y2≤1,x∈R,y∈R}则下列判断正确的是( )
A.PQR
B.PRQ
C.QPR
D.RPQ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() 取得最大值3.
取得最大值3.
(1)求![]() 的解析式及单调增区间;
的解析式及单调增区间;
(2)若![]() ,且
,且![]() ,求
,求![]() ;
;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,且
的图象,且![]() 是偶函数,求m的最小值.
是偶函数,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)问题发现
如下图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE。
填空:①∠AEB的度数为____________;
②线段AD、BE之间的数量关系是_________。

(2)拓展探究
如下图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE。请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由。

(3)解决问题
如下图,在正方形ABCD中,CD=![]() 。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。
。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com