
【题目】设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)若对于任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求出原函数的导函数,结合![]() 列方程,即可求得
列方程,即可求得![]() 的值;(2)把(1)中求得的
的值;(2)把(1)中求得的![]() 值代入函数解析式,由
值代入函数解析式,由![]() ,得到
,得到![]() ,构造函数
,构造函数![]() ,即
,即![]() ,然后对
,然后对![]() 分类讨论,求导利用导数研究函数的单调性与最值,从而可得
分类讨论,求导利用导数研究函数的单调性与最值,从而可得![]() 的取值范围.
的取值范围.
试题解析:(1)f′(x)=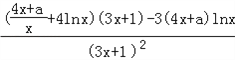 ,由题设f′(1)=1,∴
,由题设f′(1)=1,∴![]() ,∴a=0.
,∴a=0.
(2)![]() ,x∈[1,+∞),f(x)≤m(x﹣1),即4lnx≤m(3x﹣
,x∈[1,+∞),f(x)≤m(x﹣1),即4lnx≤m(3x﹣![]() ﹣2)
﹣2)
设g(x)=4lnx﹣m(3x﹣![]() ﹣2),即x∈[1,|+∞),g(x)≤0,
﹣2),即x∈[1,|+∞),g(x)≤0,
∴g′(x)=![]() ﹣m(3+
﹣m(3+![]() )=
)=![]() ,g′(1)=4﹣4m
,g′(1)=4﹣4m
①若m≤0,g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾
②若m∈(0,1),当x∈(1,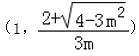 ,g′(x)>0,g(x)单调递增,g(x)≥g(1)=0,与题设矛盾.
,g′(x)>0,g(x)单调递增,g(x)≥g(1)=0,与题设矛盾.
③若m≥1,当x∈(1,+∞),),g′(x)≤0,g(x)单调递减,g(x)≤g(1)=0,即不等式成立 综上所述,m≥1.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
写出直线![]() 的方程,利用原点到直线
的方程,利用原点到直线![]() 的距离,以及
的距离,以及![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值,进而求得椭圆的方程.
的值,进而求得椭圆的方程.
椭圆右顶点坐标为![]() ,上顶点坐标为
,上顶点坐标为![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,依题意原点到直线的距离为
,依题意原点到直线的距离为![]() ,且
,且![]() ,由此解得
,由此解得![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,故选D.
,故选D.
【点睛】
本小题主要考查过两点的直线方程,考查点到直线的距离公式,考查椭圆标准方程的求法,考查了方程的思想.属于中档题.
【题型】单选题
【结束】
11
【题目】若实数![]() ,
,![]() 满足
满足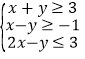 ,则
,则![]() 的最小值是( )
的最小值是( )
A. 0 B. ![]() C. -6 D. -3
C. -6 D. -3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点![]() 到两定点
到两定点![]() 和
和![]() 的距离之和为4.
的距离之和为4.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和
和![]() 的倾斜角均为
的倾斜角均为![]() ,直线
,直线![]() 过坐标原点
过坐标原点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 是交于
是交于![]() ,
, ![]() 两点,求证:对任意
两点,求证:对任意![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和半径
的垂直平分线和半径![]() 相交于
相交于![]() .
.
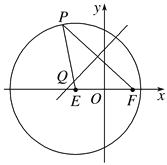
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 是轨迹
是轨迹![]() 的三个动点,点
的三个动点,点![]() 在一象限,
在一象限, ![]() 与
与![]() 关于原点对称,且
关于原点对称,且![]() ,问
,问![]() 的面积是否存在最小值?若存在,求出此最小值及相应直线
的面积是否存在最小值?若存在,求出此最小值及相应直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
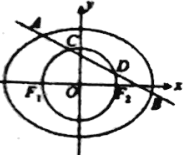
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)若直线![]() :
: ![]() 与椭圆交于
与椭圆交于![]() ,
, ![]() 两点,与以
两点,与以![]() 为直径的圆交于
为直径的圆交于![]() ,
, ![]() 两点,且满足
两点,且满足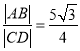 ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com