Question

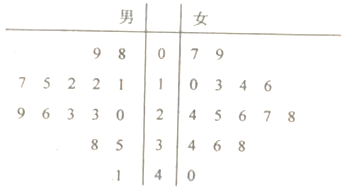
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查：在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工，对其“每十天累计看手机时间”（单位：小时）进行调查，得到茎叶图如下．所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】阅读茎叶图可得，

男职工看手机时间长度为：8,9,11,12,12,15,17,20,23,23,26,29,35,38,41,

女职工看手机时间长度为：7,9,10,13,14,16,24,25,26,27,28,34,36,38,40,

据此可得：所抽取的男职工“每十天累计看手机时间”的平均值为：

,

所抽取的女生 “每十天累计看手机时间”的中位数分别是25.

本题选择A选项.