
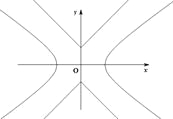
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
【答案】见解析
【解析】
(1)C1的左焦点为![]() ,过F的直线
,过F的直线![]() 与C1交于
与C1交于![]() ,与C2交于
,与C2交于![]() ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为![]() ;
;
(2)直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]() ;
;
直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]()
故直线![]() 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
(3)显然过圆![]() 内一点的直线
内一点的直线![]() 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线![]() 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点![]() ,则
,则
![]()
直线![]() 与圆
与圆![]() 内部有交点,故
内部有交点,故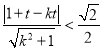
化简得,![]() ①
①
若直线![]() 与曲线C1有交点,则
与曲线C1有交点,则
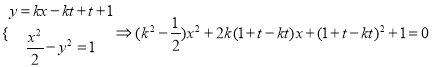
![]()
化简得,![]() ②
②
由①②得,![]()
但此时,因为![]() ,即①式不成立;
,即①式不成立;
当![]() 时,①式也不成立
时,①式也不成立
综上,直线![]() 若与圆
若与圆![]() 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点,
即圆![]() 内的点都不是“C1-C2型点” .
内的点都不是“C1-C2型点” .


科目:高中数学 来源: 题型:
【题目】(3’+7’+8’)已知以a1为首项的数列{an}满足:an+1=.
(1)当a1=1,c=1,d=3时,求数列{an}的通项公式;
(2)当0<a1<1,c=1,d=3时,试用a1表示数列{an}的前100项的和S100;
(3)当0<a1<(m是正整数),c=,d≥3m时,求证:数列a2-,a3m+2-,a6m+2-,a9m+2-成等比数列当且仅当d=3m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的左、右焦点分别为F1、F2,点P(﹣1,
1(a>b>0)的左、右焦点分别为F1、F2,点P(﹣1,![]() )在椭圆C上,且|PF2|
)在椭圆C上,且|PF2|![]() .
.
(1)求椭圆C的方程;
(2)过点F2的直线l与椭圆C交于A,B两点,M为线段AB的中点,若椭圆C上存在点N,满足![]() 3
3![]() (O为坐标原点),求直线l的方程.
(O为坐标原点),求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)若椭圆![]() 的焦距为1,求椭圆
的焦距为1,求椭圆![]() 的方程;
的方程;
(2)设![]() 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,![]() 为椭圆
为椭圆![]() 上的第一象限内的点,直线
上的第一象限内的点,直线![]() 交
交![]() 轴与点
轴与点![]() ,并且
,并且![]() ,证明:当
,证明:当![]() 变化时,点
变化时,点![]() 在某定直线上.
在某定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() l(a>b>0)经过点(
l(a>b>0)经过点(![]() ,1),且离心率e
,1),且离心率e![]() .
.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相交于AB两点,且满足∠AOB=90°(O为坐标原点),求|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,
为其焦点,![]() 为其准线,过
为其准线,过![]() 任作一条直线交抛物线于
任作一条直线交抛物线于![]() 两点,
两点,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 为
为![]() 的中点,给出下列命题:
的中点,给出下列命题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 与
与![]() 的交点的
的交点的![]() 轴上;(5)
轴上;(5)![]() 与
与![]() 交于原点.
交于原点.
其中真命题的序号为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com