
【题目】已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =![]() ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = ![]() ,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.

(1)若以F、B、C、D为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(2)当 ![]() 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
【答案】(1) ![]() 有最大值为
有最大值为![]() ;(2) 二面角的余弦值为:-
;(2) 二面角的余弦值为:-![]() .
.
【解析】试题分析:(1)由![]() 平面
平面![]() ,
, ![]() ,可得
,可得![]() ,进而由面面垂直的性质定理得到
,进而由面面垂直的性质定理得到![]() 平面
平面![]() ,进而建立空间坐标系
,进而建立空间坐标系![]() ,可得
,可得![]() 的解析式,根据二次函数的性质,易求出
的解析式,根据二次函数的性质,易求出![]() 有最大值;(2)根据(1)的结论平面
有最大值;(2)根据(1)的结论平面![]() 的一个法向量为
的一个法向量为![]() ,利用向量垂直数量积为零列方程组求出平面
,利用向量垂直数量积为零列方程组求出平面![]() 的法向量,代入向量夹角公式即可得到二面角
的法向量,代入向量夹角公式即可得到二面角![]() 的余弦值.
的余弦值.
试题解析:(1)∵平面![]() 平面
平面![]() ,AE⊥EF,
,AE⊥EF,
∴AE⊥面平面![]() ,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz.则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),
,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz.则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),
E(0,0,0)∵AD∥面BFC,
所以![]() VA-BFC=
VA-BFC=![]()
![]()
![]() ,即
,即![]() 时
时![]() 有最大值为
有最大值为![]() .
.
(2)设平面DBF的法向量为![]() ,∵AE=2, B(2,0,0),
,∵AE=2, B(2,0,0),
D(0,2,2),F(0,3,0),∴![]()
![]() (-2,2,2),
(-2,2,2),
则 ,即
,即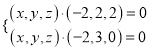 ,
, ![]()
取x=3,则y=2,z=1,∴![]()
面BCF的一个法向量为![]()
则cos<![]() >=
>=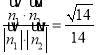 .
.
由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为:-![]()


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】某研究性学习小组为了解学生每周用于体育锻炼时间的情况,在甲、乙两所学校随机抽取了各50名学生,做问卷调查,并作出如下频率分布直方图: 
(1)根据直方图计算:两所学校被抽取到的学生每周用于体育锻炼时间的平均数;
(2)在这100名学生中,要从每周用于体育锻炼时间不低于10小时的学生中选出3人,该3人中来自乙学校的学生数记为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱中ABC﹣A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1. 
(1)证明:AC1⊥平面A1BC;
(2)求二面角B﹣A1C﹣B1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为p2= ![]() ,定点A(0,﹣
,定点A(0,﹣ ![]() ),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
(1)求圆锥曲线C的直角坐标方程和直线l的参数方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M||F1N|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥C的底面是正方形,PA⊥平面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PEC
(2)求证:平面PCD⊥平面PEC;
(3)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度,某中学团委以问卷形式调查了![]() 位家长,得到如下统计表:
位家长,得到如下统计表:
男性家长 | 女性家长 | 合计 | |
赞成 |
|
|
|
无所谓 |
|
|
|
合计 |
|
|
|
(1)据此样本,能否有![]() 的把握认为“接受程度”与家长性别有关?说明理由;
的把握认为“接受程度”与家长性别有关?说明理由;
(2)学校决定从男性家长中按分层抽样方法选出![]() 人参加今年的高中学生成人礼仪式,并从中选
人参加今年的高中学生成人礼仪式,并从中选![]() 人交流发言,求发言人中至多一人持“赞成”态度的概率.
人交流发言,求发言人中至多一人持“赞成”态度的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com