
【题目】已知递增数列{an}前n项和为Sn,且满足a1=3,4Sn﹣4n+1=an2,设bn![]() (n∈N*)且数列{bn}的前n项和为Tn
(n∈N*)且数列{bn}的前n项和为Tn
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若对任意的n∈N*,不等式λTn![]() n
n![]() (﹣1)n+1恒成立,求实数λ的取值范围.
(﹣1)n+1恒成立,求实数λ的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)(﹣∞,14).
【解析】
(Ⅰ)当n≥2时,由4Sn﹣4n+1=an2,类比可得4Sn﹣1﹣4(n﹣1)+1=an﹣12,两式相减,再化简整理可得(an+an﹣1﹣2)(an﹣an﹣1﹣2)=0,即an+an﹣1﹣2=0,或an﹣an﹣1﹣2=0,根据数列{an}是递增数列可排除不符合题意的一项,即可证明结论;
(Ⅱ)先根据第(Ⅰ)题的结果计算出数列{an}的通项公式,以及数列{bn}的通项公式,然后运用裂项相消法计算出Tn的表达式,将Tn的表达式代入不等式,分离参变量可得λ![]() (2n+3)[3n+2(﹣1)n+1],构造数列{cn}:令cn
(2n+3)[3n+2(﹣1)n+1],构造数列{cn}:令cn![]() (2n+3)[3n+2(﹣1)n+1],通过分别对数列{cn}的奇偶项的单调性进行分析可得数列{cn}的最小项的值,即可得到实数λ的取值范围.
(2n+3)[3n+2(﹣1)n+1],通过分别对数列{cn}的奇偶项的单调性进行分析可得数列{cn}的最小项的值,即可得到实数λ的取值范围.
(Ⅰ)证明:依题意,当n≥2时,由4Sn﹣4n+1=an2,可得
4Sn﹣1﹣4(n﹣1)+1=an﹣12,
两式相减,可得
4an﹣4=an2﹣an﹣12,
化简整理,得
(an+an﹣1﹣2)(an﹣an﹣1﹣2)=0,
∴an+an﹣1﹣2=0,或an﹣an﹣1﹣2=0,
∵数列{an}是递增数列,
∴an≥an﹣1,则an+an﹣1≥2an﹣1≥2a1=2×3=6,
∴an+an﹣1﹣2=0不符合题意,
∴an﹣an﹣1﹣2=0,即an﹣an﹣1=2,
∴数列{an}是首项为3,公差为2的等差数列.
(Ⅱ)由(Ⅰ)知,an=3+2(n﹣1)=2n+1,n∈N*,
则bn![]() (
(![]() ),
),
故Tn=b1+b2+…+bn
![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)
![]() (
(![]() )
)
![]() (
(![]() )
)
![]() ,
,
将Tn![]() 代入不等式,可得λ
代入不等式,可得λ![]() n
n![]() (﹣1)n+1,
(﹣1)n+1,
化简整理,得
λ![]() (2n+3)[3n+2(﹣1)n+1],
(2n+3)[3n+2(﹣1)n+1],
构造数列{cn}:令cn![]() (2n+3)[3n+2(﹣1)n+1],则
(2n+3)[3n+2(﹣1)n+1],则
①当n为奇数时,n+2为奇数,
cn![]() (2n+3)[3n+2(﹣1)n+1]
(2n+3)[3n+2(﹣1)n+1]![]() (2n+3)(3n+2),
(2n+3)(3n+2),
cn+2![]() [2(n+2)+3][3(n+2)+2(﹣1)n+3]
[2(n+2)+3][3(n+2)+2(﹣1)n+3]![]() (2n+7)(3n+8),
(2n+7)(3n+8),
cn+2﹣cn![]() (2n+7)(3n+8)
(2n+7)(3n+8)![]() (2n+3)(3n+2)
(2n+3)(3n+2)
![]()
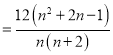 ,
,
∵n为奇数,∴n2+2n﹣1![]() 0,
0,
∴![]() 0,即cn+2
0,即cn+2![]() cn,
cn,
∴数列{cn}的奇数项为单调递增数列,即c1![]() c3
c3![]() c5
c5![]() …
…
②当n为偶数时,n+2也为偶数,
cn![]() (2n+3)[3n+2(﹣1)n+1]
(2n+3)[3n+2(﹣1)n+1]![]() (2n+3)(3n﹣2),
(2n+3)(3n﹣2),
cn+2![]() [2(n+2)+3][3(n+2)+2(﹣1)n+3]
[2(n+2)+3][3(n+2)+2(﹣1)n+3]![]() (2n+7)(3n+4),
(2n+7)(3n+4),
cn+2﹣cn![]() (2n+7)(3n+4)
(2n+7)(3n+4)![]() (2n+3)(3n﹣2)
(2n+3)(3n﹣2)
![]() 0,
0,
故数列{cn}的偶数项为单调递增数列,即c2![]() c4
c4![]() c6
c6![]() …
…
∵c1=25,c2=14,c3=33,c4![]() ,
,
∴λ![]() {cn}min=c2=14,
{cn}min=c2=14,
∴实数λ的取值范围为(﹣∞,14).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
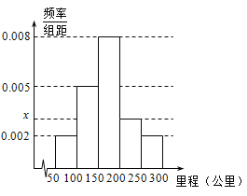
(1)求直方图中![]() 的值;
的值;
(2)求![]() 辆纯电动汽车续驶里程的中位数;
辆纯电动汽车续驶里程的中位数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程为
辆车,求其中恰有一辆车的续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
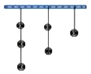
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某市国庆节7天假期的楼房认购量与成交量的折线图,小明同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.则上述判断正确的个数为( )
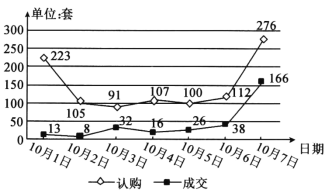
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定平面上的五个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
A. 120种 B. 125种 C. 130种 D. 135种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com