
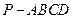 中,顶点
中,顶点 在底面
在底面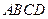 上的射影恰好落在
上的射影恰好落在 的中点
的中点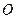 上,又∠
上,又∠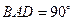 ,
,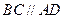 ,且
,且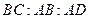
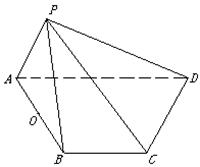
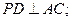
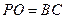 , 求直线
, 求直线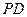 与
与 所成的角的余弦值;
所成的角的余弦值;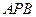 与平面
与平面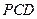 所成的角为
所成的角为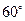 , 求
, 求 的值
的值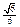
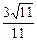
 中点
中点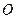 为点
为点 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以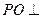 底面
底面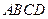 . 以
. 以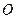 为坐标原点,
为坐标原点,  所在直线为
所在直线为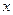 轴,
轴, 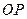 所在直线为
所在直线为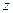 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系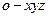
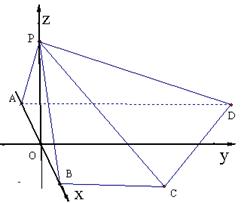
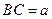 , OP = h则依题意得:
, OP = h则依题意得: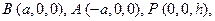
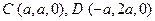 .
. 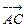 =
= 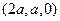 ,
, 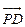 =
= 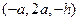 ,
, 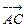 ·
·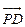 =
= 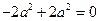 , ∴
, ∴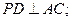
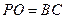 , 得h =" a," 于是
, 得h =" a," 于是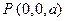 ,
, 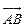 =
= 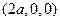 ,
, 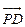 =
= 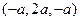 , ∴
, ∴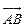 ·
·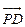 =
= 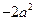 ,
, 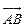 ,
,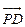 > =
> = 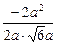 =
=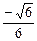 , ∴ 直线
, ∴ 直线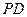 与
与 所成的角的余弦值为
所成的角的余弦值为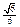 ;
; 的法向量为m, 可得m =" (0,1,0" ),
的法向量为m, 可得m =" (0,1,0" ),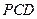 的法向量为n =
的法向量为n = 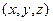 , 由
, 由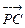 =
= 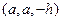 ,
, 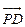 =
= 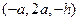 ,
, 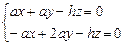 , 解得n =" (1," 2 ,
, 解得n =" (1," 2 ,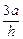 ), ∴ m•n =" 2" ,
), ∴ m•n =" 2" ,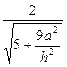 , ∵ 二面角为
, ∵ 二面角为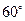 , ∴
, ∴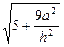 = 4,
= 4,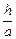 =
=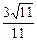 ,即
,即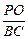 =
=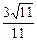 . --- 5分
. --- 5分

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:不详 题型:解答题
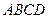 、
、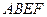 的边长都是1,平面
的边长都是1,平面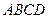
 平面
平面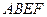 ,点
,点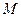 在
在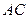 上移动,点
上移动,点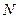 在
在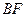 上移动,若
上移动,若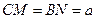 (
(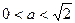 )
)
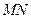 的长;
的长;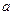 为何值时,
为何值时,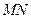 的长最小;
的长最小;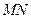 的长最小时,求面
的长最小时,求面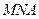 与面
与面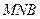 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
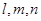 是三条不重合的直线,
是三条不重合的直线, 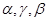 是三个不重合的平面,下列四个命题正确的个数为 ( )
是三个不重合的平面,下列四个命题正确的个数为 ( )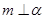 , m∥
, m∥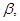
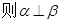
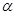 所成的角相等,则m∥n;
所成的角相等,则m∥n;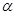 ,m//
,m//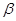 ,n∥β,则
,n∥β,则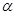 //
//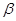 ;
;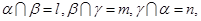
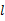 ∥
∥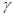 ,则m∥n.
,则m∥n.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
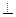 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,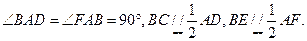

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
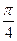 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
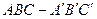 的
的 底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达
底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达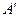 点,则小虫所行的最短路程为__________cm
点,则小虫所行的最短路程为__________cm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com