
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态,一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:车辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
, ![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2 | 1.9 | 1.7 | ||
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 |
| 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放,根据市场调查,这个城市投放8千辆时,该公司平均一辆单一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6,问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入—成本).
【答案】(1) 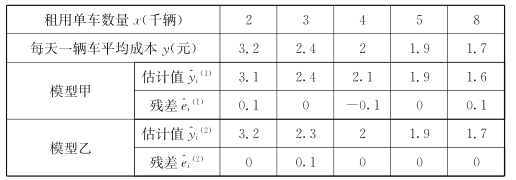 ,
, ![]() ,
, ![]() ,
, ![]() ,模型乙的拟合效果更好;(2) 投放1万辆能获得更多利润,应该增加到投放1万辆.
,模型乙的拟合效果更好;(2) 投放1万辆能获得更多利润,应该增加到投放1万辆.
【解析】试题分析(1)①通过对回归方程的计算可得两种模型的估计值![]() ,代入
,代入![]() ,即可得残差;②计算可得
,即可得残差;②计算可得![]() 可知模型乙拟合效果更好;(2)分别计算投放
可知模型乙拟合效果更好;(2)分别计算投放![]() 千辆和一万辆时该公司一天获得的总利润,即可得结论。
千辆和一万辆时该公司一天获得的总利润,即可得结论。
(1)①经计算,可得下表:

②![]() ,
, ![]() ,
,
![]() ,故模型乙的拟合效果更好.
,故模型乙的拟合效果更好.
(2)若投放量为8千辆,则公司获得每辆车一天的收入期望为![]() ,
,
所以一天的总利润为![]() (元)
(元)
若投放量为1万辆,由(1)可知,每辆车的成本为![]() (元),
(元),
每辆车一天收入期望为![]() ,
,
所以一天的总利润为![]() (元)
(元)
所以投放1万辆能获得更多利润,应该增加到投放1万辆.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数y= ![]() 的定义域是( )
的定义域是( )
A.[﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() ]
]
B.(﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() )??
)??
C.[﹣2,﹣1)∪(1,2]
D.(﹣2,﹣1)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
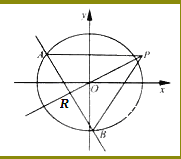
【题目】如图,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点O的直线
.不过原点O的直线![]() 与C相交于A,B两点,且线段AB被直线OP平分.
与C相交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+bx﹣alnx.
(1)若x=2是函数f(x)的极值点,1和x0是函数f(x)的两个不同零点,且x0∈(n,n+1),n∈N,求n.
(2)若对任意b∈[﹣2,﹣1],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课程表上的相邻两节文化课之间最多间隔1节艺术课的概率为(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在30人或30人以下,每人需交费用为900元;若旅行团人数多于30人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数75人为止.旅行社需支付各种费用共计15000元.
(1)写出每人需交费用y关于人数x的函数;
(2)旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如下表:
投资股市 | 获利 | 不赔不赚 | 亏损 | 购买基金 | 获利 | 不赔不赚 | 亏损 | |
概率 |
|
|
| 概率 |
|
|
|
(Ⅰ)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“买基金”,若一年后他们中至少有一人盈利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,某人现有
,某人现有![]() 万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com