
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再将所有点的横坐标缩短到原来的
个单位,再将所有点的横坐标缩短到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像则下面对函数
的图像则下面对函数![]() 的叙述不正确的是( )
的叙述不正确的是( )
A.函数![]() 的周期
的周期![]()
B.函数![]() 的一个对称中心
的一个对称中心![]()
C.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
D.当![]() ,
,![]() 时,函数
时,函数![]() 有最小值
有最小值![]()
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
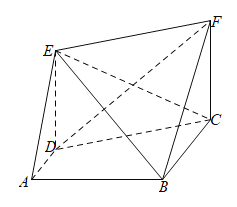
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(3)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子中有5个大小相同的球,其中3个白球与2个黑球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任意取出一个球,则第一次为白球、第二次为黑球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
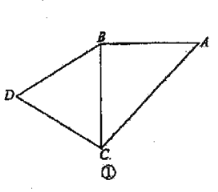
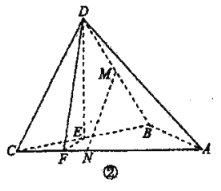
【题目】如图①,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 是等边三角形,
是等边三角形,![]() ,如图②,将
,如图②,将![]() 沿
沿![]() 折起使平面
折起使平面![]() 平面
平面![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下两个图表是2019年初的4个月我国四大城市的居民消费价格指数(上一年同月![]() )变化图表,则以下说法错误的是( )
)变化图表,则以下说法错误的是( )
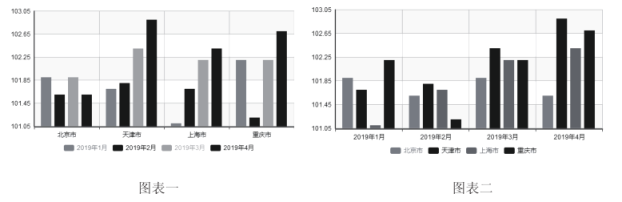
(注:图表一每个城市的条形图从左到右依次是1、2、3、4月份;图表二每个月份的条形图从左到右四个城市依次是北京、天津、上海、重庆)
A.3月份四个城市之间的居民消费价格指数与其它月份相比增长幅度较为平均
B.4月份仅有三个城市居民消费价格指数超过102
C.四个月的数据显示北京市的居民消费价格指数增长幅度波动较小
D.仅有天津市从年初开始居民消费价格指数的增长呈上升趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() ,
, ![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
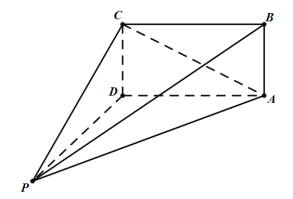
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com