
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)证明:![]() .
.
【答案】(1)所求切线方程为![]() ;(2)
;(2)![]()
【解析】
试题(1)先求出导函数![]() ,根据对数的几何意义可得切线斜率,利用点斜式可得切线方程;(2)要证
,根据对数的几何意义可得切线斜率,利用点斜式可得切线方程;(2)要证![]() ,只需证
,只需证![]() ,利用导数研究两函数的单调性,从而求出两函数的最值即可证明
,利用导数研究两函数的单调性,从而求出两函数的最值即可证明![]() ,进而可得结论.
,进而可得结论.
试题解析:(1)因为![]() ,
,
所以![]() ,
,
因为![]() ,所以曲线
,所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)证明:要证![]() ,只需证
,只需证![]() ,
,
设![]() ,
,
则![]() ,
,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
从而![]() ,即
,即![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线、利用导数研究函数的单调性进而求最值以及利用导数证明不等式,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() 两点,
两点,![]() 是该抛物线上位于第一象限内的点.
是该抛物线上位于第一象限内的点.

(Ⅰ) 记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
(Ⅱ)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() 关于
关于![]() 轴的对称点恰好在直线
轴的对称点恰好在直线![]() 上,求
上,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
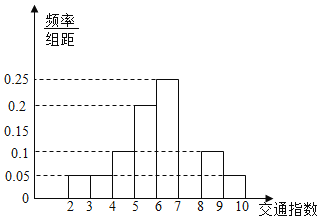
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
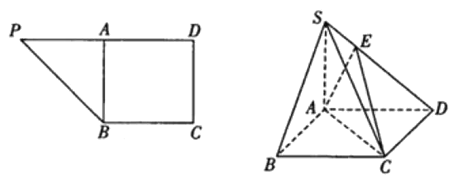
(1)求证:SA⊥平面ABCD;
(2)若E为SD中点,求D点到面EAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如右图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方
向滚动,M和N是小圆的一条固定直径的两个端点.那么,当小圆这
样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A. B.
B.
C. D.
D.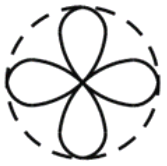
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蝴蝶定理因其美妙的构图,像是一只翩翩起舞的蝴蝶,一代代数学名家蜂拥而证,正所谓花若芬芳蜂蝶自来.如图,已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() .原点
.原点![]() 在圆
在圆![]() 内.
内.

(1)求证:![]() .
.
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
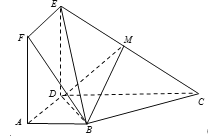
(Ⅰ) 若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 当平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com