
分析 (1)点(2,f(2))处的切线的斜率为1,即f′(2)=1,可求a值,解关于导函数的不等式,求出函数的单调区间即可,
(2)求出g(x)的解析式,由t∈[0,1],且g(x)在区间(t,2)上总存在极值,得到关于m的不等式组,于是可求m的范围.
解答 解:∵f(x)=a(lnx-x)-3,x>0,
∴f′(x)=a($\frac{1}{x}$-1),f′(2)=-$\frac{a}{2}$=1,解得a=-2,
∴f(x)=-2lnx+2x-3,f′(x)=$\frac{2(x-1)}{x}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)g(x)=x3+($\frac{m}{2}$+2)x2-2x,
∴g′(x)=3x2+(m+4)x-2
∵g(x)在区间(t,2)上总存在极值,且g′(0)=-2
∴$\left\{\begin{array}{l}{g′(t)<0}\\{g′(2)>0}\end{array}\right.$,
由题意知:对于任意的t∈[0,1],g′(t)<0恒成立,
所以有:$\left\{\begin{array}{l}{g′(0)=-2<0}\\{g′(1)<0}\\{g′(2)>0}\end{array}\right.$,∴-9<m<-5.
∴当m∈(-9,-5)内取值时对于任意的t∈[0,1],
函数g(x)=x3+x2[$\frac{m}{2}$+f′(x)]在区间(t,2)上总存在极值.
点评 本题考查利用函数的导数来求函数的单调区间,以及已知函数曲线上一点求曲线的切线方程,考查求导公式的掌握情况,含参数的数学问题的处理,构造函数求解证明不等式问题.


科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
已知圆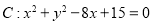 ,直线
,直线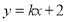 上至少存在一点
上至少存在一点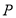 ,使得以点
,使得以点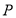 为原心,半径为1的圆与圆
为原心,半径为1的圆与圆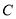 有公共点,则
有公共点,则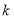 的最小值是( )
的最小值是( )
A.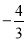 B.
B.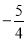 C.
C.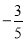 D.
D.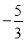
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
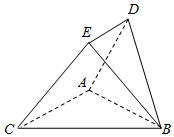 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
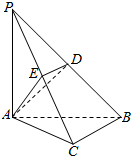 如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com