
| A. |  | B. |  | ||
| C. |  | D. | 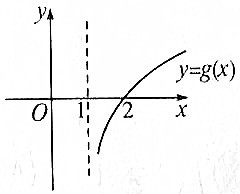 |
分析 由函数f(x)=ax+ka-x,(a>0,a≠1)在(-∞,+∞)上既是奇函数,又是增函数,则由复合函数的性质,我们可得k=-1,a>1,由此不难判断函数的图象.
解答 解:∵函数f(x)=ax+ka-x,(a>0,a≠1)在(-∞,+∞)上是奇函数
∴f(-x)+f(x)=0
即(k+1)(ax+a-x)=0
则k=-1
又∵函数f(x)=ax+ka-x,(a>0,a≠1)在(-∞,+∞)上是增函数
则a>1
则g(x)=loga(x+k)=loga(x-1)
函数图象必过(2,0),且为增函数
故选:D.
点评 若函数在其定义域为为奇函数,则f(-x)+f(x)=0,若函数在其定义域为为偶函数,则f(-x)-f(x)=0,这是函数奇偶性定义的变形使用,另外函数单调性的性质,在公共单调区间上:增函数-减函数=增函数也是解决本题的关键.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.
在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com