
ΓΨΧβΡΩΓΩ‘ΎΕ§ΦΨΘ§”…”Ύ ήΒΫΒΆΈ¬ΚΆΥΣΕ≥ΒΡ”ΑœλΘ§ Ώ≤ΥΒΡΦέΗώΜαΥφΉ≈–η«σΝΩΒΡ‘ωΦ”ΕχΧα…ΐ.“―÷ΣΡ≥Ι©”Π…ΧœρΖΙΒξΕ®ΤΎΙ©”ΠΡ≥÷÷ Ώ≤ΥΘ§ΤδΦέΗώΜαΥφΉ≈»’–η«σΝΩΒΡ‘ωΦ”Εχ…œ…ΐΘ§ΨΏΧε«ι–ΈΆ≥ΦΤ»γœ¬±μΥυ ΨΘΚ

Θ®1Θ©ΗυΨί…œ±μ÷–ΒΡ ΐΨίΫχ––≈–ΕœΘ§![]() ”κ
”κ![]() ΡΡ“ΜΗωΗϋ ΚœΉςΈΣ»’Ι©”ΠΝΩ
ΡΡ“ΜΗωΗϋ ΚœΉςΈΣ»’Ι©”ΠΝΩ![]() ”κΒΞΦέ
”κΒΞΦέ![]() ÷°ΦδΒΡΜΊΙιΖΫ≥ΧΘΜΘ®Ηχ≥ω≈–ΕœΦ¥Ω…Θ§≤Μ±ΊΥΒΟςάμ”…Θ©ΘΜ
÷°ΦδΒΡΜΊΙιΖΫ≥ΧΘΜΘ®Ηχ≥ω≈–ΕœΦ¥Ω…Θ§≤Μ±ΊΥΒΟςάμ”…Θ©ΘΜ
Θ®2Θ©ΗυΨίΘ®1Θ©ΒΡ≈–ΕœΫαΙϊ“‘ΦΑ≤ΈΩΦ ΐΨίΘ§Ϋ®ΝΔ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΒΡΜΊΙιΖΫ≥ΧΘΜ
Θ®3Θ©ΗΟΒΊ«χ”–![]() ΗωΨΤΒξΘ§Τδ÷–
ΗωΨΤΒξΘ§Τδ÷–![]() ΗωΨΤΒξΟΩ»’Ε‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ
ΗωΨΤΒξΟΩ»’Ε‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ![]() “‘œ¬Θ§
“‘œ¬Θ§![]() ΗωΨΤΒξΕ‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ
ΗωΨΤΒξΕ‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ![]() “‘…œΘ§¥”’β
“‘…œΘ§¥”’β![]() ΗωΨΤΒξ÷–»Έ»Γ
ΗωΨΤΒξ÷–»Έ»Γ![]() ΗωΫχ––Βς≤ιΘ§«σ«Γ”–
ΗωΫχ––Βς≤ιΘ§«σ«Γ”–![]() ΗωΨΤΒξΕ‘ Ώ≤Υ–η«σΝΩ‘Ύ
ΗωΨΤΒξΕ‘ Ώ≤Υ–η«σΝΩ‘Ύ![]() “‘…œΒΡΗ≈¬ .
“‘…œΒΡΗ≈¬ .
≤ΈΩΦΙΪ ΫΦΑ ΐΨίΘΚ
Ε‘”Ύ“ΜΉι ΐΨί![]() Θ§
Θ§![]() ...
...![]() Θ§ΤδΜΊΙι÷±œΏ
Θ§ΤδΜΊΙι÷±œΏ![]() ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣ
ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣ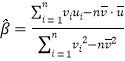 Θ§
Θ§![]()

Τδ÷–ΘΚ![]() Θ§
Θ§ ![]()
ΓΨ¥πΑΗΓΩΘ®1Θ©―Γ‘ώ![]() Θ®2Θ©
Θ®2Θ©![]() Θ®3Θ©
Θ®3Θ©![]()
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©―Γ‘ώ![]() ΉςΈΣ»’Ι©”ΠΝΩ
ΉςΈΣ»’Ι©”ΠΝΩ![]() ”κ
”κ![]() ÷°ΦδΒΡΜΊΙιΖΫ≥ΧΗϋ ΚœΘΜΘ®2Θ©Ε‘
÷°ΦδΒΡΜΊΙιΖΫ≥ΧΗϋ ΚœΘΜΘ®2Θ©Ε‘![]() ΝΫ±ΏΆ§ ±»ΓΉ‘»ΜΕ‘ ΐΒΟ
ΝΫ±ΏΆ§ ±»ΓΉ‘»ΜΕ‘ ΐΒΟ![]() Θ§Νν
Θ§Νν![]() Θ§
Θ§![]() ΒΟ
ΒΟ![]() Θ§Ι
Θ§Ι 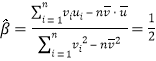 Θ§
Θ§![]() Θ§
Θ§![]() Θ§¥”ΕχΩ…ΒΟΫαΙϊΘΜΘ®3Θ©άϊ”ΟΝ–ΨΌΖ®Θ§¥”’β
Θ§¥”ΕχΩ…ΒΟΫαΙϊΘΜΘ®3Θ©άϊ”ΟΝ–ΨΌΖ®Θ§¥”’β![]() ΗωΨΤΒξ÷–»Έ»Γ
ΗωΨΤΒξ÷–»Έ»Γ![]() ΗωΙ≤
ΗωΙ≤![]() ÷÷Θ§«Γ”–
÷÷Θ§«Γ”–![]() ΗωΨΤΒξΕ‘ Ώ≤Υ–η«σΝΩ‘Ύ
ΗωΨΤΒξΕ‘ Ώ≤Υ–η«σΝΩ‘Ύ![]() “‘…œΒΡ”–
“‘…œΒΡ”–![]() ÷÷Θ§ΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ ΫΩ…ΒΟΫαΙϊ.
÷÷Θ§ΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ ΫΩ…ΒΟΫαΙϊ.
œξΫβΘΚΘ®1Θ©―Γ‘ώ![]() ΉςΈΣ»’Ι©”ΠΝΩ
ΉςΈΣ»’Ι©”ΠΝΩ![]() ”κ
”κ![]() ÷°ΦδΒΡΜΊΙιΖΫ≥ΧΗϋ Κœ.
÷°ΦδΒΡΜΊΙιΖΫ≥ΧΗϋ Κœ.
Θ®2Θ©Ε‘![]() ΝΫ±ΏΆ§ ±»ΞΉ‘»ΜΕ‘ ΐΒΟ
ΝΫ±ΏΆ§ ±»ΞΉ‘»ΜΕ‘ ΐΒΟ![]() ΘΜ
ΘΜ
Νν![]() Θ§
Θ§![]() ΒΟ
ΒΟ![]() Θ§Ι
Θ§Ι 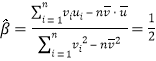 Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Ι Υυ«σΖΫ≥ΧΈΣ![]() .
.
Θ®3Θ©“άΧβ“βΘ§![]() ΗωΨΤΒξΟΩ»’Ε‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ
ΗωΨΤΒξΟΩ»’Ε‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ![]() “‘œ¬Θ§Φ«ΈΣ
“‘œ¬Θ§Φ«ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΗωΨΤΒξΕ‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ
ΗωΨΤΒξΕ‘ Ώ≤ΥΒΡ–η«σΝΩ‘Ύ![]() “‘…œΘ§Φ«ΈΣ
“‘…œΘ§Φ«ΈΣ![]() Θ§
Θ§![]() Θ§‘ρ»Έ»Γ
Θ§‘ρ»Έ»Γ![]() ΗωΨΤΒξΘ§Υυ”–ΒΡ«ιΩωΈΣ
ΗωΨΤΒξΘ§Υυ”–ΒΡ«ιΩωΈΣ
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Ι≤
Θ§Ι≤![]() ÷÷Θ§
÷÷Θ§
Τδ÷–¬ζΉψΧθΦΰΒΡ”–![]() ÷÷Θ§Ι Υυ«σΗ≈¬
÷÷Θ§Ι Υυ«σΗ≈¬ ![]() .
.


 ΩΎΥψΧβΧλΧλΝΖœΒΝ–¥πΑΗ
ΩΎΥψΧβΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=|x+a|+|x©¹2|
Θ®1Θ©Β±a=©¹3 ±Θ§«σ≤ΜΒ» ΫfΘ®xΘ©Γί3ΒΡΫβΦ·ΘΜ
Θ®2Θ©»τfΘ®xΘ©Γή|x©¹4|ΒΡΫβΦ·ΑϋΚ§[1Θ§2]Θ§«σaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=4cosxsinΘ®x+![]() Θ©-1Θ°
Θ©-1Θ°
Θ®1Θ©«σfΘ®xΘ©ΒΡΉν–Γ’ΐ÷ήΤΎΚΆΒΞΒςΒίΦθ«χΦδΘΜ
Θ®2Θ©ΫΪy=fΘ®xΘ©ΆΦœσ…œΥυ”–ΒΡΒψœρ”“ΤΫ––“ΤΕ·![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫy=gΘ®xΘ©ΒΡΆΦœσΘ°»τgΘ®xΘ©‘ΎΘ®0Θ§mΘ©ΡΎ «ΒΞΒςΚ· ΐΘ§«σ Β ΐmΒΡΉν¥σ÷ΒΘ°
ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫy=gΘ®xΘ©ΒΡΆΦœσΘ°»τgΘ®xΘ©‘ΎΘ®0Θ§mΘ©ΡΎ «ΒΞΒςΚ· ΐΘ§«σ Β ΐmΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΟϋΧβpΘΚxΓ [1Θ§2]Θ§ ![]() ©¹lnx©¹aΓί0Θ§ΟϋΧβqΘΚx0Γ RΘ§ ΙΒΟx02+2ax0©¹8©¹6aΓή0Θ§»γΙϊΟϋΧβΓΑpΜρqΓ± «’φΟϋΧβΘ§ΟϋΧβΓΑp«“qΓ± «ΦΌΟϋΧβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
©¹lnx©¹aΓί0Θ§ΟϋΧβqΘΚx0Γ RΘ§ ΙΒΟx02+2ax0©¹8©¹6aΓή0Θ§»γΙϊΟϋΧβΓΑpΜρqΓ± «’φΟϋΧβΘ§ΟϋΧβΓΑp«“qΓ± «ΦΌΟϋΧβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=x©¹1+ ![]() Θ®aΓ RΘ©Θ°
Θ®aΓ RΘ©Θ°
Θ®1Θ©»τ«ζœΏy=fΘ®xΘ©‘ΎΒψΘ®1Θ§fΘ®1Θ©Θ©¥ΠΒΡ«–œΏΤΫ––”Ύx÷αΘ§«σaΒΡ÷ΒΘΜ
Θ®2Θ©«σΚ· ΐfΘ®xΘ©ΒΡΦΪ÷ΒΘΜ
Θ®3Θ©Β±a=1 ±Θ§»τ÷±œΏlΘΚy=kx©¹1”κ«ζœΏy=fΘ®xΘ©ΟΜ”–ΙΪΙ≤ΒψΘ§«σkΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –”–AΓΔBΝΫΦ“”πΟΪ«ρ«ρΨψά÷≤ΩΘ§ΝΫΦ“…η±ΗΚΆΖΰΈώΕΦΚήΚΟΘ§ΒΪ ’Ζ―ΖΫ Ϋ≤ΜΆ§Θ§AΨψά÷≤ΩΟΩΩι≥ΓΒΊΟΩ–Γ ± ’Ζ―6‘ΣΘΜBΨψά÷≤ΩΑ¥‘¬ΦΤΖ―Θ§“ΜΗω‘¬÷–20–Γ ±“‘ΡΎ![]() Κ§20–Γ ±
Κ§20–Γ ±![]() ΟΩΩι≥ΓΒΊ ’Ζ―90‘ΣΘ§≥§Ιΐ20–Γ ±ΒΡ≤ΩΖ÷Θ§ΟΩΩι≥ΓΒΊΟΩ–Γ ±2‘ΣΘ§Ρ≥Τσ“ΒΉΦ±Ηœ¬Ηω‘¬¥”’βΝΫΦ“Ψψά÷≤Ω÷–ΒΡ“ΜΦ“Ήβ”Ο“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·Θ§ΤδΜνΕ· ±Φδ≤Μ…Ό”Ύ12–Γ ±Θ§“≤≤Μ≥§Ιΐ30–Γ ±Θ°
ΟΩΩι≥ΓΒΊ ’Ζ―90‘ΣΘ§≥§Ιΐ20–Γ ±ΒΡ≤ΩΖ÷Θ§ΟΩΩι≥ΓΒΊΟΩ–Γ ±2‘ΣΘ§Ρ≥Τσ“ΒΉΦ±Ηœ¬Ηω‘¬¥”’βΝΫΦ“Ψψά÷≤Ω÷–ΒΡ“ΜΦ“Ήβ”Ο“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·Θ§ΤδΜνΕ· ±Φδ≤Μ…Ό”Ύ12–Γ ±Θ§“≤≤Μ≥§Ιΐ30–Γ ±Θ°
![]() …η‘ΎAΨψά÷≤ΩΉβ“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·x–Γ ±ΒΡ ’Ζ―ΈΣ
…η‘ΎAΨψά÷≤ΩΉβ“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·x–Γ ±ΒΡ ’Ζ―ΈΣ![]() ‘Σ
‘Σ![]() Θ§‘ΎBΨψά÷≤ΩΉβ“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·x–Γ ±ΒΡ ’Ζ―ΈΣ
Θ§‘ΎBΨψά÷≤ΩΉβ“ΜΩι≥ΓΒΊΩΣ’ΙΜνΕ·x–Γ ±ΒΡ ’Ζ―ΈΣ![]() ‘Σ
‘Σ![]() Θ§ ‘«σ
Θ§ ‘«σ![]() ”κ
”κ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
![]() Έ ΗΟΤσ“Β―Γ‘ώΡΡΦ“Ψψά÷≤Ω±»ΫœΚœΥψΘ§ΈΣ ≤Ο¥ΘΩ
Έ ΗΟΤσ“Β―Γ‘ώΡΡΦ“Ψψά÷≤Ω±»ΫœΚœΥψΘ§ΈΣ ≤Ο¥ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ≥Θ ΐ
≥Θ ΐ![]() Θ°
Θ°
![]() ÷ΛΟς
÷ΛΟς![]() ‘Ύ
‘Ύ![]() …œ «ΦθΚ· ΐΘ§‘Ύ
…œ «ΦθΚ· ΐΘ§‘Ύ![]() …œ «‘ωΚ· ΐΘΜ
…œ «‘ωΚ· ΐΘΜ
![]() Β±
Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
![]() Ε‘”Ύ
Ε‘”Ύ![]() ÷–ΒΡΚ· ΐ
÷–ΒΡΚ· ΐ![]() ΚΆΚ· ΐ
ΚΆΚ· ΐ![]() Θ§»τΕ‘»Έ“β
Θ§»τΕ‘»Έ“β![]() Θ§Ήή¥φ‘Ύ
Θ§Ήή¥φ‘Ύ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ≥…ΝΔΘ§«σ Β ΐaΒΡ÷ΒΘ°
≥…ΝΔΘ§«σ Β ΐaΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΦ·ΚœA={x|x2-7x+6ΘΦ0}Θ§B={x|4-tΘΦxΘΦt}Θ§RΈΣ Β ΐΦ·Θ°
Θ®1Θ©Β±t=4 ±Θ§«σAΓ»BΦΑAΓ…RBΘΜ
Θ®2Θ©»τAΓ»B=AΘ§«σ Β ΐtΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤CΒΡ‘≤–Ρ‘Ύ÷±œΏ…œ![]() Θ§«“”κ÷±œΏ
Θ§«“”κ÷±œΏ![]() œύ«–”ΎΒψ
œύ«–”ΎΒψ![]()
Θ®1Θ©«σ‘≤CΒΡΖΫ≥ΧΘΜ
Θ®2Θ© «Ζώ¥φ‘ΎΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ‘≤CΫΜ”Ύ
”κ‘≤CΫΜ”Ύ![]() ΝΫΒψΘ§«“
ΝΫΒψΘ§«“![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ®OΈΣΉχ±ξ‘≠ΒψΘ©Θ§»τ¥φ‘ΎΘ§«σ≥ω÷±œΏ
Θ®OΈΣΉχ±ξ‘≠ΒψΘ©Θ§»τ¥φ‘ΎΘ§«σ≥ω÷±œΏ![]() ΒΡΖΫ≥ΧΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΖΫ≥ΧΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com