
| A. | m=-$\sqrt{3}$,n=-2 | B. | m=$\sqrt{3}$,n=2 | C. | m=$\sqrt{3}$,n=-2 | D. | m=-$\sqrt{3}$,n=2 |
分析 根据题意,设直线mx+$\frac{n}{2}$y-1=0为直线l,由直线的一般式方程分析可得:直线$\sqrt{3}x-y-3\sqrt{3}$=0的斜率k=$\sqrt{3}$,倾斜角为60°,结合题意可得直线l的倾斜角为120°,进而可得其斜率,又由其在y轴上的截距是-1,可得直线l的方程,结合直线的方程分析可得答案.
解答 解:根据题意,设直线mx+$\frac{n}{2}$y-1=0为直线l,
另一直线的方程为$\sqrt{3}x-y-3\sqrt{3}$=0,
变形可得y=$\sqrt{3}$(x-3),其斜率k=$\sqrt{3}$,
则其倾斜角为60°,
而直线l的倾斜角是直线$\sqrt{3}x-y-3\sqrt{3}$=0的倾斜角的2倍,
则直线l的倾斜角为120°,
且斜率k=tan120°=-$\sqrt{3}$,
又由l在y轴上的截距是-1,则其方程为y=-$\sqrt{3}$x-1;
又由其一般式方程为mx+$\frac{n}{2}$y-1=0,
分析可得:m=-$\sqrt{3}$,n=-2;
故选:A.
点评 本题考查直线的斜截式方程,关键是由直线的倾斜角求出直线的斜率.


科目:高中数学 来源: 题型:解答题
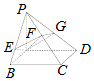 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F查看答案和解析>>
科目:高中数学 来源: 题型:填空题
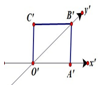 如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.
如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
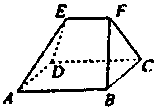 如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )
如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )| A. | $\frac{9}{2}$ | B. | 5 | C. | 6 | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).
如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0<0,ln(x0+1)<0 | B. | ?x0≤0,ln(x0+1)≤0 | C. | ?x0>0,ln(x0+1)<0 | D. | ?x0>0,ln(x0+1)≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com