
分析 (1)由条件求出φ(x)以及定义域,由求导公式和法则求出导函数,化简后确定导数恒大于0,即可求出函数φ (x)的单调区间;
(2)先由导数的几何意义和点斜式方程求出直线l的方程,再设l与曲线y=g(x)相切于点(x1,${e}^{{x}_{1}}$),同理表示出直线l的方程,对比后可得lnx0-1=$\frac{1}{{x}_{0}}$(lnx0+1 ),求出lnx0=$\frac{{x}_{0}+1}{{x}_{0}-1}$,由(1)中知φ(x)的单调性,求出φ(e)、φ(e2)并判断出符号,结合零点存在性定理可得在(1,+∞)上x0存在且唯一.
解答 解:(1)由题意得,φ(x)=f(x)-$\frac{x+1}{x-1}$=lnx-$\frac{x+1}{x-1}$,
∴φ(x)的定义域是(0,1)∪(1,+∞),
且φ′(x)=$\frac{1}{x}$-$\frac{(x+1)′(x-1)-(x+1)(x-1)′}{(x-1)^{2}}$
=$\frac{1}{x}+\frac{2}{(x-1)^{2}}$=$\frac{{x}^{2}+1}{{x(x-1)}^{2}}$>0,
∵x>0且x≠1,∴φ'(x)>0,
∴函数φ(x)的单调递增区间为(0,1)和(1,+∞);
(2)假设在区间(1,+∞)上存在x0满足条件,
∵f′(x)=$\frac{1}{x}$,则f′(x0)=$\frac{1}{{x}_{0}}$,
∴切线l的方程为y-lnx0=$\frac{1}{{x}_{0}}$(x-x0),即y=$\frac{1}{{x}_{0}}$x+lnx0-1,①
设直线l与曲线y=g(x)相切于点(x1,${e}^{{x}_{1}}$),
∵g′(x)=ex,∴${e}^{{x}_{1}}$=$\frac{1}{{x}_{0}}$,则x1=-lnx0,
∴直线l方程又为y-$\frac{1}{{x}_{0}}$=$\frac{1}{{x}_{0}}$(x+lnx0),即y=$\frac{1}{{x}_{0}}$x+$\frac{1}{{x}_{0}}$lnx0+$\frac{1}{{x}_{0}}$,②
由①②得lnx0-1=$\frac{1}{{x}_{0}}$(lnx0+1 ),得lnx0=$\frac{{x}_{0}+1}{{x}_{0}-1}$,
下面证明在区间(1,+∞)上x0存在且唯一.
由(1)可知,φ(x)=lnx-$\frac{x+1}{x-1}$在区间(1,+∞)上递增.
又φ(e)=lne-$\frac{e+1}{e-1}$=$\frac{-2}{e-1}$<0,φ(e2)=lne2-$\frac{{e}^{2}+1}{{e}^{2}-1}$=$\frac{{e}^{2}-3}{{e}^{2}-1}$>0,
结合零点存在性定理知:φ(x)=0必在区间(e,e2)上有唯一的根x0,
∴在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
点评 本题考查利用导数研究在曲线上某点处的切线方程,导数与函数单调性的关系,函数零点存在性定理等应用,考查转化思想,分析、解决问题的能力.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
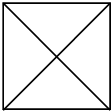 已知某几何体的俯视图是如图所示的正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,x2=-1 | B. | ?x∈R,x2=-1 | C. | ?x∉R,x2=-1 | D. | ?x∈R,x2=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-3或x>-2} | B. | {x|x<-$\frac{1}{2}$或x>-$\frac{1}{3}$} | C. | {x|-$\frac{1}{2}$<x<-$\frac{1}{3}$} | D. | {x|-3<x<-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (${\frac{1}{3}$,1) | B. | (${\frac{1}{2}$,1) | C. | (-${\frac{2}{3}$,1) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com