
【题目】函数f(x)=![]() (cosx﹣sinx)sin(x+
(cosx﹣sinx)sin(x+![]() )﹣2asinx+b(a>0).
)﹣2asinx+b(a>0).
(1)若b=1,且对任意![]() , 恒有f(x)>0,求a的取值范围;
, 恒有f(x)>0,求a的取值范围;
(2)若f(x)的最大值为1,最小值为﹣4,求实数a,b的值.
【答案】解:(1)当b=1时,函数式可化简如下:
f(x)=![]() (cosx﹣sinx)(cosx+sinx)﹣2asinx+1
(cosx﹣sinx)(cosx+sinx)﹣2asinx+1
=![]() (cos2x﹣sin2x)﹣2asinx+1=﹣sin2x﹣2asinx+
(cos2x﹣sin2x)﹣2asinx+1=﹣sin2x﹣2asinx+![]() ,
,
令t=sinx(0<t<![]() ),对任意x∈(0,
),对任意x∈(0,![]() ),恒有f(x)>0,
),恒有f(x)>0,
即为﹣t2﹣2at+![]() >0,分离参数得:﹣2a>t﹣
>0,分离参数得:﹣2a>t﹣![]() ,
,
由t﹣![]() 在(0,
在(0,![]() )递增,所以,t﹣
)递增,所以,t﹣![]() <
<![]() ﹣3=﹣
﹣3=﹣![]() ,
,
因此,﹣2a>﹣![]() ,解得,0<a<
,解得,0<a<![]() ,
,
即实数a的取值范围为(0,![]() );
);
(2)f(x)=﹣sin2x﹣2asinx+b+![]() ,令t=sinx(﹣1≤t≤1),
,令t=sinx(﹣1≤t≤1),
记g(t)=﹣t2﹣2at+b+![]() ,图象的对称轴t=﹣a<0,且开口向下,
,图象的对称轴t=﹣a<0,且开口向下,
①当﹣a≤﹣1时,即a≥1,函数g(t)在[﹣1,1]上单调递减,则
g(t)max=g(﹣1)=﹣1+2a+b+![]() =1,
=1,
g(t)min=g(1)=﹣1﹣2a+b+![]() =﹣4,
=﹣4,
解得a=![]() ,b=﹣1;
,b=﹣1;
②当﹣1<﹣a<1时,即0<a<1,函数g(t)在[﹣1,1]上先增后减,则
g(x)max=g(﹣a)=![]() +b+a2=1,
+b+a2=1,
g(x)min=g(1)=﹣1﹣2a+b+![]() =﹣4,
=﹣4,
解方程可得a=![]() ﹣1,b=2
﹣1,b=2![]() ﹣
﹣![]() ,由于a=
,由于a=![]() ﹣1>1,不合题意,舍去.
﹣1>1,不合题意,舍去.
综上可得a=![]() ,b=﹣1.
,b=﹣1.
【解析】(1)先化简函数式,将函数化为sinx的二次型函数,再用分离参数法和单调性求解;
(2)讨论二次函数在“动轴定区间”上的最值,再列方程求解.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.过平面外一点作这个平面的垂面有且只有一个
B.过直线外一点作这条直线的平行平面有且只有一个
C.过直线外一点作这条直线的垂线有且只有一条
D.过平面外的一条斜线作这个平面的垂面有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤![]() )的部分图象,其图象与y轴交于点(0,
)的部分图象,其图象与y轴交于点(0,![]() )
)
(Ⅰ)求函数的解析式;
(Ⅱ)若![]() , 求
, 求![]() -
-![]() 的值.
的值.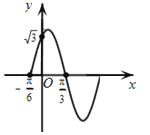
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|1﹣![]() |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
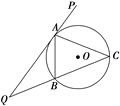
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,它们在
,它们在![]() 轴右侧有两个交点
轴右侧有两个交点![]() 、
、![]() ,满足
,满足![]() .将直线
.将直线![]() 左侧的椭圆部分(含
左侧的椭圆部分(含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() ,直线
,直线![]() 右侧的双曲线部分(不含
右侧的双曲线部分(不含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() .以
.以![]() 为端点作一条射线,分别交
为端点作一条射线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (点
(点![]() 在第一象限),设此时
在第一象限),设此时![]() .
.
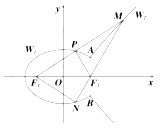
(1)求![]() 的方程;
的方程;
(2)证明: ![]() ,并探索直线
,并探索直线![]() 与
与![]() 斜率之间的关系;
斜率之间的关系;
(3)设直线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com