
【题目】已知函数![]() (
(![]() )是偶函数.
)是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 没有零点,求
没有零点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,
, ![]() 的最小值为0,求实数
的最小值为0,求实数![]() 的值.
的值.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
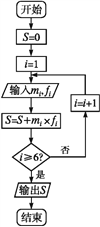
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )的图象过点B(0,﹣1),且在(
)的图象过点B(0,﹣1),且在( ![]() ,
, ![]() )上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当x1 , x2∈(﹣
)上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
),且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
A.﹣ ![]()
B.﹣1
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
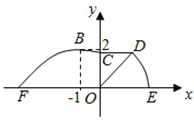
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】<中华人民共和国个人所得税法>规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:

(1)若某人一月份应缴纳此项税款为280元,那么他当月的工资、薪金所得是多少?
(2)假设某人一个月的工资、薪金所得是![]() 元(0<
元(0<![]() 10000),试将其当月应缴纳此项税款
10000),试将其当月应缴纳此项税款![]() 元表示成关于
元表示成关于![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电商中“猫狗大战”在节日期间的竞争异常激烈,在刚过去的618全民年中购物节中,某东当日交易额达1195亿元,现从该电商“剁手党”中随机抽取100名顾客进行回访,按顾客的年龄分成了6组,得到如下所示的频率直方图. 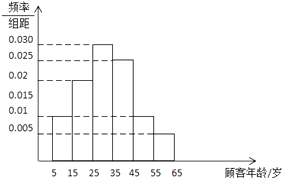
(1)求顾客年龄的众数,中位数,平均数(每一组数据用中点做代表);
(2)用样本数据的频率估计总体分布中的概率,则从全部顾客中任取3人,记随机变量X为顾客中年龄小于25岁的人数,求随机变量X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到点
到点![]() 的最短路线长为
的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为
的交点为![]() .
.

(1)求三棱柱![]() 的体积;
的体积;
(2)证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com