
【题目】如图,三棱柱![]() 的所有棱长均为2,平面
的所有棱长均为2,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)证明: ![]() ;
;
(2)若![]() 是棱
是棱![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2) 所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】试题分析:(1)证线线垂直,由平面![]() 平面
平面![]() 得
得![]() 平面
平面![]() ,再由底面图形得线线垂直.(2)建系求面的法向量,得法向量的夹角.
,再由底面图形得线线垂直.(2)建系求面的法向量,得法向量的夹角.
解:
(1)证明:取![]() 中点
中点![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
, ![]() ,依题意得
,依题意得![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为四边形![]() 为菱形,所以
为菱形,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解:由(1)结合已知得: ![]() ,
, ![]() ,
, ![]() ,
,
以![]() 为原点,如图所示建立空间直角坐标系
为原点,如图所示建立空间直角坐标系![]() ,因为侧面
,因为侧面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 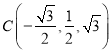 ,
,
所以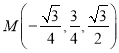 ,
, ![]() ,
, 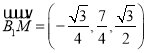 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由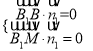 得
得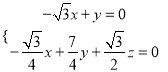 ,令
,令![]() ,可取
,可取![]() ,
,
而平面![]() 的一个法向量
的一个法向量![]() ,由图可知二面角
,由图可知二面角![]() 为锐角,
为锐角,
因为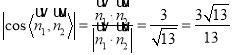 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知函数f(x)=2cos x(sin x+cos x).
(1)求f![]() 的值;
的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at﹣1(a>0,且a≠1),它的图象如图所示.给出以下命题: ①池塘中原有浮草的面积是0.5m2;
②到第7个月浮草的面积一定能超过60m2
③浮草每月增加的面积都相等;
④若浮草面积达到4m2 , 16m2 , 64m2所经过时间分别为t1 , t2 , t3 , 则t1+t2<t3 , 其中所有正确命题的序号是( )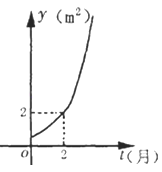
A.①②
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一条公路上,每隔100km有个仓库(如图),共有5个仓库.一号仓库存有10t货物,二号仓库存20t,五号仓库存40t,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输1km需要0.5元运输费,那么要多少才行? ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为该椭圆的右焦点,过点
为该椭圆的右焦点,过点![]() 任作一直线
任作一直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]() 的最大值为4.
的最大值为4.
(1)求椭圆![]() 的方程;
的方程;
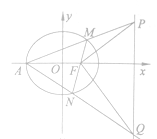
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是 ![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com