
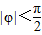 )
)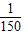 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?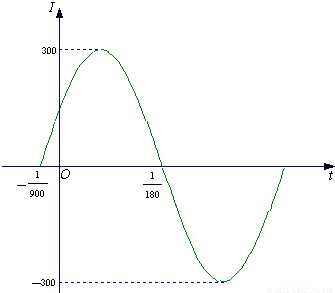
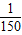 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤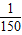 ,则易求出满足条件的ω值.
,则易求出满足条件的ω值.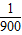 ,t2=
,t2=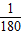 ,
,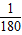 +
+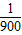 )=
)=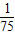 .…(4分)
.…(4分)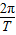 =150π. 又当t=
=150π. 又当t=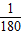 时,I=0,即sin(150π•
时,I=0,即sin(150π•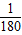 +φ)=0,
+φ)=0,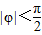 ,∴φ=
,∴φ=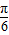 .…(6分)
.…(6分)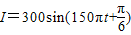 .…(8分)
.…(8分)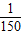 ,即
,即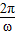 ≤
≤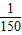 ,(ω>0)
,(ω>0)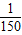 ,进而构造关于ω的不等式.
,进而构造关于ω的不等式. 

 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
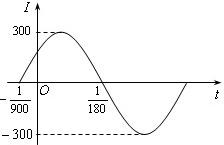 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).| π |
| 2 |
| 1 |
| 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
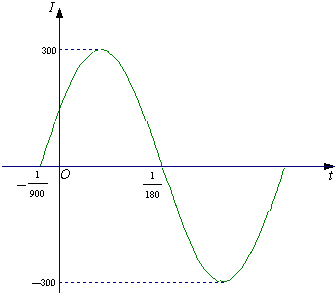 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).| π |
| 2 |
| 1 |
| 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:
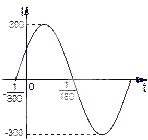 已知电流I与时间t的关系式为I=Asin(ωx+φ).
已知电流I与时间t的关系式为I=Asin(ωx+φ).| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省深圳市高级中学高三(上)第二次测试数学试卷(文科)(解析版) 题型:解答题
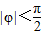 )在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;
)在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;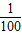 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?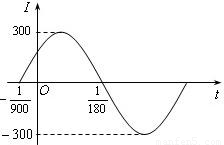
查看答案和解析>>
科目:高中数学 来源:2010-2011年陕西省汉中市汉台区高一下学期期末数学 题型:解答题
(13分)已知电流I与时间t的关系式为 。
。
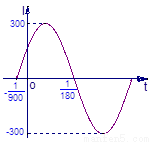
(1)右图是 (ω>0,
(ω>0, )在一个周期内的图象,根据图中数据求
)在一个周期内的图象,根据图中数据求  的解析式;
的解析式;
(2)记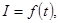 求
求 的单调递增区间
的单调递增区间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com