
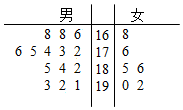
 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作. 分析 (1)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取8人,每个人被抽中的概率是$\frac{8}{20}$=$\frac{2}{5}$.根据茎叶图,“甲部门”人选有10人,“乙部门”人选有10人.可得所以选中的“甲部门”人选,“乙部门”人选.设事件A“至少有一名甲部门人被选中”,其对立事件为$\overline{A}$.P(A)=1-P($\overline{A}$).
(2)依据题意,所选毕业生中能担任“助理工作”的人数X的取值分别为0,1,2,3,利用“超几何分布”即可得出.
解答 解:(1)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取8人,每个人被抽中的概率是$\frac{8}{20}$=$\frac{2}{5}$.
根据茎叶图,“甲部门”人选有10人,“乙部门”人选有10人.
所以选中的“甲部门”人选有$10×\frac{2}{5}$=4人,“乙部门”人选有10×$\frac{2}{5}$=4人.
设事件A“至少有一名甲部门人被选中”,其对立事件为$\overline{A}$.
P(A)=1-P($\overline{A}$)=1-$\frac{{∁}_{4}^{3}}{{∁}_{8}^{3}}$=$\frac{13}{14}$.
因此,至少有1人是“甲部门”人选的概率是$\frac{13}{14}$.
(2)依据题意,所选毕业生中能担任“助理工作”的人数X的取值分别为0,1,2,3,
P(X=0)=$\frac{{∁}_{6}^{0}{∁}_{4}^{3}}{{∁}_{10}^{3}}$=$\frac{1}{30}$,
P(X=1)=$\frac{{∁}_{6}^{1}{∁}_{4}^{2}}{{∁}_{10}^{3}}$=$\frac{3}{10}$,
P(X=2)=$\frac{{∁}_{6}^{3}{∁}_{4}^{1}}{{∁}_{10}^{3}}$=$\frac{1}{2}$,
P(X=3)=$\frac{{∁}_{6}^{3}{∁}_{4}^{0}}{{∁}_{10}^{3}}$=$\frac{1}{6}$.
因此,X的分布列如下:
所以X的数学期望EX=0×$\frac{1}{30}$+1×$\frac{3}{10}$+2×$\frac{1}{2}$+3×$\frac{1}{6}$=$\frac{9}{5}$.
点评 本题考查了超几何分布列其的数学期望计算公式、分层抽样、相互对立事件的概率计算公式,考查了推理能力与计算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 算法与求解一个问题的方法相同 | |
| B. | 算法只能解决一个问题,不能重复使用 | |
| C. | 算法过程要一步一步执行 | |
| D. | 有的算法执行完以后,可能没有结果 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com