Question

10．已知α，β是方程2x²+2ax+b=0的两根，且α∈[0，1]，β∈[1，2]，a，b∈R，则$\frac{{5{a^2}+4ab+{b^2}}}{{2{a^2}+ab}}$的范围[2，$\frac{5}{2}$]．

Answer 1

分析 化简可得$\frac{2a+b}{a}$+$\frac{a}{2a+b}$，从而化为判断函数y=x+$\frac{1}{x}$的单调性，再确定$\frac{2a+b}{a}$的取值范围，由题意知$\left\{\begin{array}{l}{b≥0}\\{2+2a+b≤0}\\{8+4a+b≥0}\end{array}\right.$，从而利用线性规划确定$\frac{2a+b}{a}$∈[$\frac{2}{3}$，2]，从而解得．

解答 解：∵$\frac{{5{a^2}+4ab+{b^2}}}{{2{a^2}+ab}}$=$\frac{（2a+b）^{2}+{a}^{2}}{a（2a+b）}$
=$\frac{2a+b}{a}$+$\frac{a}{2a+b}$，
∵α，β是方程2x²+2ax+b=0的两根，且α∈[0，1]，β∈[1，2]，
∴$\left\{\begin{array}{l}{b≥0}\\{2+2a+b≤0}\\{8+4a+b≥0}\end{array}\right.$，
作平面区域如下，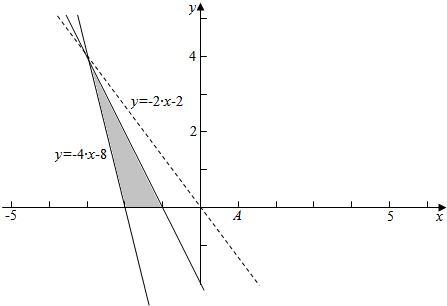
，
$\frac{y}{x}$的几何意义是点（x，y）与点（0，0）的连线的斜率，
结合图象可知，-$\frac{4}{3}$≤$\frac{y}{x}$≤0，
故-$\frac{4}{3}$≤$\frac{b}{a}$≤0，
故$\frac{2a+b}{a}$∈[$\frac{2}{3}$，2]，
而y=x+$\frac{1}{x}$在[$\frac{2}{3}$，1）上单调递减，在[1，2]上单调递增；
且$\frac{2}{3}$+$\frac{3}{2}$=$\frac{13}{6}$，1+1=2，2+$\frac{1}{2}$=$\frac{5}{2}$；
故$\frac{2a+b}{a}$+$\frac{a}{2a+b}$∈[2，$\frac{5}{2}$]；
故答案为：[2，$\frac{5}{2}$]．

点评 本题考查了学生的化简运算能力与线性规划的应用，同时考查了对勾函数的应用及数形结合的思想应用．