
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
B.( ![]() ,1)
,1)
C.( ![]() )
)
D.(﹣∞,﹣ ![]() ,)
,) ![]()
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两名同学的数学学习情况,对他们的![]() 次数学测试成绩(满分
次数学测试成绩(满分![]() 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中![]() 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是![]() ,乙同学成绩的平均分是
,乙同学成绩的平均分是![]() 分.
分.
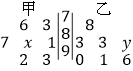
(1)求![]() 和
和![]() 的值;
的值;
(2)现从成绩在![]() 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1:ρsin2θ=4cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C2的参数方程为: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲线C:
]),曲线C: 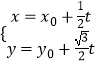 (t为参数).
(t为参数).
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)C与C1相交于A,B,与C2相切于点Q,求|AQ|﹣|BQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为![]() ,
,![]() ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() .若用每天
.若用每天![]() 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 的表达式,并规定当
的表达式,并规定当![]() 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当![]() 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(UA)∩B=( )
A.?
B.{x| ![]() <x≤1}
<x≤1}
C.{x|x<1}
D.{x|0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺作样本,检测其某项质量指标,检测结果如频率分布直方图所示.
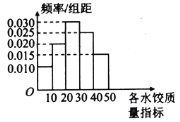
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() 和方差
和方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若该品牌的速冻水饺的某项质量指标Z服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求Z落在![]() 内的概率;
内的概率;
② 若某人从某超市购买了1包这种品牌的速冻水饺,发现该包速冻水饺某项质量指标值为55,根据![]() 原则判断该包速冻水饺某项质量指标值是否正常
原则判断该包速冻水饺某项质量指标值是否正常
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
(I)求证:直线DE⊥平面PAC.
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.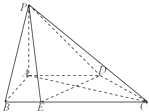
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2 , 若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
A. 289 B. 1 024 C. 1 225 D. 1 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com