
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()

(Ⅰ)证明:![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(解法1)(Ⅰ)因为![]() 底面
底面![]() ,所以
,所以![]() ,
,
由底面![]() 为长方形,有
为长方形,有![]() ,而
,而![]() ,
,
所以![]() .而
.而![]() ,所以
,所以![]() .
.
又因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .而
.而![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可知四面体
,可知四面体![]() 的四个面都是直角三角形,
的四个面都是直角三角形,
即四面体![]() 是一个鳖臑,其四个面的直角分别为
是一个鳖臑,其四个面的直角分别为![]()
![]() .
.
(Ⅱ)如图1,在面![]() 内,延长
内,延长![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 是平面
是平面![]() 与平面
与平面![]()
的交线.由(Ⅰ)知,![]() ,所以
,所以![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .而
.而![]() ,所以
,所以![]() .
.
故![]() 是面
是面![]() 与面
与面![]() 所成二面角的平面角,
所成二面角的平面角,
设![]() ,
,![]() ,有
,有![]() ,
,
在Rt△PDB中, 由![]() , 得
, 得![]() ,
,
则![]() , 解得
, 解得![]() .
.
所以![]()
故当面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() 时,
时,![]() .
.
(解法2)
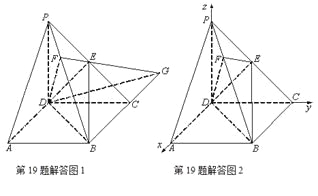
(Ⅰ)如图2,以![]() 为原点,射线
为原点,射线![]() 分别为
分别为![]() 轴的正半轴,建立空间直角坐标系.
轴的正半轴,建立空间直角坐标系.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
于是![]() ,即
,即![]() .
.
又已知![]() ,而
,而![]() ,所以
,所以![]() .
.
因![]() ,
,![]() , 则
, 则![]() , 所以
, 所以![]() .
.
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可知四面体
,可知四面体![]() 的四个面都是直角三角形,
的四个面都是直角三角形,
即四面体![]() 是一个鳖臑,其四个面的直角分别为
是一个鳖臑,其四个面的直角分别为![]()
![]() .
.
(Ⅱ)由![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
由(Ⅰ)知,![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,
,
则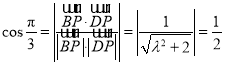 ,
,
解得![]() .所以
.所以![]()
故当面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】若x4(x+4)8=a0+a1(x+3)+a2(x+3)2+…+a12(x+3)12,则log2(a1+a3+…+a11)=( ).
A. 4B. 8C. 12D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,BCD是边长为![]() 的等边三角形,
的等边三角形,![]() ,二面角A﹣BC﹣D的大小为θ,且
,二面角A﹣BC﹣D的大小为θ,且![]() ,则三棱锥A﹣BCD体积的最大值为( )
,则三棱锥A﹣BCD体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率是40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下10组随机数:907 966 191 925 271 431 932 458 569 683.
据此估计,该运动员三次投篮恰有两次命中的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,我市积极打造“绿城”的创建目标,使城市环境绿韵萦绕,使市民生活绿意盎然.有效增加城区绿化面积,提高城区绿化覆盖率,提升城市形象品位.林业部门推广种植甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:

(1)根据茎叶图求甲、乙两种树苗的平均高度;
(2)根据茎叶图,计算甲、乙两种树苗的高度的方差,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程与离心率;
的方程与离心率;
(Ⅱ)设椭圆![]() 上不与
上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是定值.
轴截得的弦长是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com