
分析 根据正弦函数的定义域,我们构造关于x的不等式,解不等式,求出自变量x的取值范围,即可得到函数y=tan($\frac{π}{4}$-2x)的定义域.
解答 解:要使函数y=tan($\frac{π}{4}$-2x)的解析式有意义,
自变量x须满足:2x-$\frac{π}{4}$≠kπ+$\frac{π}{2}$,k∈Z,
解得:x≠$\frac{kπ}{2}$+$\frac{3}{8}$π,k∈Z,
故函数y=tan($\frac{π}{4}$-2x)的定义域为{x|x≠$\frac{kπ}{2}$+$\frac{3}{8}$π,k∈Z}
故答案为:{x|x≠$\frac{kπ}{2}$+$\frac{3}{8}$π,k∈z}.
点评 本题考查的知识点是正切函数的定义域,其中根据正切函数的定义域,构造关于x的不等式是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | -log20172016 | B. | -1 | C. | log20172016-1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (-∞,4] | C. | [4,+∞) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,4] | B. | [-2,2] | C. | [-2,0] | D. | [0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴负半轴上的角是零角 | |
| B. | 三角形的内角必是第一、二象限内的角 | |
| C. | 不相等的角的终边一定不相同 | |
| D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
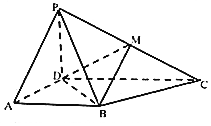 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com