
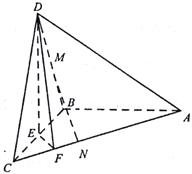
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】设m个正数a1 , a2 , …,am(m≥4,m∈N*)依次围成一个圆圈.其中a1 , a2 , a3 , …ak﹣1 , ak(k<m,k∈N*)是公差为d的等差数列,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列.
(1)若a1=d=2,k=8,求数列a1 , a2 , …,am的所有项的和Sm;
(2)若a1=d=2,m<2015,求m的最大值;
(3)是否存在正整数k,满足a1+a2+…+ak﹣1+ak=3(ak+1+ak+2+…+am﹣1+am)?若存在,求出k值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,小明想将短轴长为2,长轴长为4的一个半椭圆形纸片剪成等腰梯形ABDE,且梯形ABDE内接于半椭圆,DE∥AB,AB为短轴,OC为长半轴
(1)求梯形ABDE上底边DE与高OH长的关系式;
(2)若半椭圆上到H的距离最小的点恰好为C点,求底边DE的取值范围

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,
,![]() ,
,![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com