
【题目】有一容积为![]() 的正方体容器
的正方体容器![]() ,在棱
,在棱![]() 、
、![]() 和面对角线
和面对角线![]() 的中点各有一小孔
的中点各有一小孔![]() 、
、![]() 、
、![]() ,若此容器可以任意放置,则其可装水的最大容积是( )
,若此容器可以任意放置,则其可装水的最大容积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
分别讨论水面过直线![]() 、
、![]() 、
、![]() 时从正方体截去的几何体体积的最小值,即可得出此容器可装水的最大容积.
时从正方体截去的几何体体积的最小值,即可得出此容器可装水的最大容积.
当水面过直线![]() 时,如下图所示,
时,如下图所示,
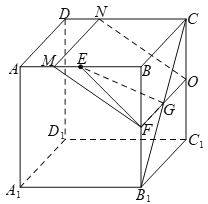
水面截去正方体![]() 所得几何体为三棱柱
所得几何体为三棱柱![]() ,
,
当点![]() 在水面上方或水面上时,容器中的水不会漏,且当点
在水面上方或水面上时,容器中的水不会漏,且当点![]() 与点
与点![]() 重合时,截去的几何体体积最小为
重合时,截去的几何体体积最小为![]() ;
;
当水面过直线![]() 时,如下图所示,
时,如下图所示,
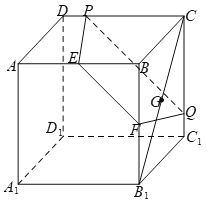
水面截去正方体![]() 所得几何体为三棱台
所得几何体为三棱台![]() ,
,
当点![]() 在水面上方或水面上时,容器中的水不会漏,且当点
在水面上方或水面上时,容器中的水不会漏,且当点![]() 在直线
在直线![]() 上时,截去的几何体为三棱柱,且体积最小为
上时,截去的几何体为三棱柱,且体积最小为![]() ;
;
当水面过直线![]() 时,如下图所示,
时,如下图所示,
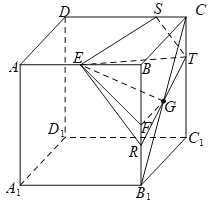
当点![]() 在水面上方或水面上时,容器中的水不会漏,此时水面截去正方体
在水面上方或水面上时,容器中的水不会漏,此时水面截去正方体![]() 所得几何体为
所得几何体为![]() ,且直线
,且直线![]() 过点
过点![]() ,易知梯形
,易知梯形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,此时,几何体
面积的一半,此时,几何体![]() 的体积为
的体积为![]() .
.
当![]() 与直线
与直线![]() 重合时,如下图所示,
重合时,如下图所示,
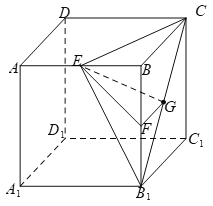
此时,点![]() 在水面上方,容器不会漏水,水面截去正方体
在水面上方,容器不会漏水,水面截去正方体![]() 所得几何体为三棱锥
所得几何体为三棱锥![]() ,
,
该三棱锥的体积为![]() .
.
综上可知,水面截去截去正方体![]() 所得几何体体积的最小值为
所得几何体体积的最小值为![]() .
.
因此,该容器可装水的最大容积是![]() .
.
故选:C.


科目:高中数学 来源: 题型:
【题目】如图所示,取同离心率的两个椭圆成轴对称内外嵌套得一个标志,为美观考虑,要求图中标记的①、②、③)三个区域面积彼此相等.(已知:椭圆面积为圆周率与长半轴、短半轴长度之积,即椭圆![]()
![]() 面积为
面积为![]() )
)
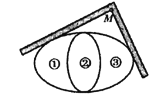
(1)求椭圆的离心率的值;
(2)已知外椭圆长轴长为6,用直角角尺两条直角边内边缘与外椭圆相切,移动角尺绕外椭圆一周,得到由点M生成的轨迹将两椭圆围起来,整个标志完成.请你建立合适的坐标系,求出点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的周期为
的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() .将函数
.将函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式.
的解析式.
(2)定义:当函数取得最值时,函数图象上对应的点称为函数的最值点,如果函数![]() 的图象上至少有一个最大值点和一个最小值点在圆
的图象上至少有一个最大值点和一个最小值点在圆![]() 的内部或圆周上,求k的取值范围.
的内部或圆周上,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,
的图象,![]() 分别是
分别是![]() 的极值点,且有
的极值点,且有![]() ,则函数
,则函数![]() ( )
( )
A.在区间![]() 上单调递增B.在区间
上单调递增B.在区间![]() 上单调递增
上单调递增
C.在区间![]() 上单调递减D.在区间
上单调递减D.在区间![]() 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的![]() 网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网络 | 月租费 | 本地话费 | 长途话费 |
甲:联通 |
|
|
|
乙:移动“神州行” | 无 |
|
|
若王先生每月拨打本地电话的时间是拨打长途电话时间的![]() 倍,若要用联通
倍,若要用联通![]() 应最少打多长时间的长途电话才合算.( )
应最少打多长时间的长途电话才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在
在![]() 上,以R为切点的D的切线的斜率为
上,以R为切点的D的切线的斜率为![]() ,过
,过![]() 外一点A(不在x轴上)作
外一点A(不在x轴上)作![]() 的切线
的切线![]()
![]() ,点BC为切点,作平行于
,点BC为切点,作平行于![]() 的切线
的切线![]() (切点为D),点MN分别是与
(切点为D),点MN分别是与![]()
![]() 的交点(如图).
的交点(如图).
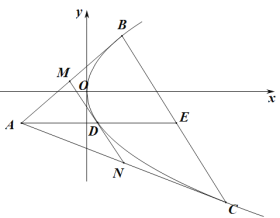
(1)用BC的纵坐标st表示直线![]() 的斜率;
的斜率;
(2)设三角形![]() 面积为S,若将由过
面积为S,若将由过![]() 外一点的两条切线及第三条切线(平行于两切线切点的连线)围成的三角形叫做“切线三角形”,如
外一点的两条切线及第三条切线(平行于两切线切点的连线)围成的三角形叫做“切线三角形”,如![]() ,再由MN作“切线三角形”,并依这样的方法不断作切线三角形…,试利用“切线三角形”的面积和计算由抛物线及
,再由MN作“切线三角形”,并依这样的方法不断作切线三角形…,试利用“切线三角形”的面积和计算由抛物线及![]() 所围成的阴影部分的面积T.
所围成的阴影部分的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解社区群众体育活动的开展情况,拟采用分层抽样的方法从A,B,C三个行政区抽出6个社区进行调查.已知A,B,C行政区中分别有12,18,6个社区.
(1)求从A,B,C三个行政区中分别抽取的社区个数;
(2)若从抽得的6个社区中随机的抽取2个进行调查结果的对比,求抽取的2个社区中至少有一个来自A行政区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com