
【题目】有能力互异的3人应聘同一公司,他们按照报名顺序依次接受面试,经理决定“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”,记该公司录用到能力最强的人的概率为p,录用到能力中等的人的概率为q,则(p,q)=( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
【答案】D
【解析】解:设三人能力分别为强,中,弱,则三人参加面试的次序为:
(强,中,弱),(强,弱,中),(中,强,弱),(中,弱,强),(弱,中,强),(弱,强,中),
即基本事件总数n=6,
按“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”的规定,
该公司录用到能力最强的人包含的基本事件有:(中,强,弱),(中,弱,强),(弱,强,中),共三种情况,
∴该公司录用到能力最强的人的概率p= ![]() =
= ![]() .
.
该公司录用到能力中等的人包含的基本事件有:(强,弱,中),(弱,中,强),共二种情况,
∴该公司录用到能力中等的人的概率q= ![]() .
.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆C: ![]() =1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
=1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
(1)证明:b2=ad;
(2)若M的坐标为( ![]() ,1),求椭圆C的方程.
,1),求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x+1|+|x﹣1|.
(1)求f(x)≤x+2的解集;
(2)若不等式f(x)≤log2(a2﹣4a+12)对任意实数a恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+ ![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是奇函数,g(x)是偶函数,且在公共定义域{x|x∈R且x≠±1}上满足f(x)+g(x)= ![]() .
.
(1)求f(x)和g(x)的解析式;
(2)设h(x)=f(x)﹣g(x),求h( ![]() );
);
(3)求值:h(2)+h(3)+h(4)+…+h(2016)+h( ![]() )+h(
)+h( ![]() )+h(
)+h( ![]() )+…+h(
)+…+h( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数是同一函数的是( )
① ![]() 与
与 ![]() ;
;
②f(x)=|x|与 ![]() ;
;
③f(x)=x0与g(x)=1;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②
B.①③
C.②④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
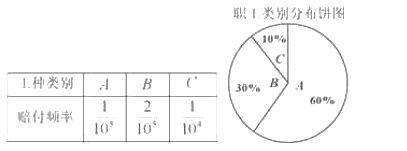
【题目】某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
对于![]() 、
、![]() 、
、![]() 三类工种职工每人每年保费分别为
三类工种职工每人每年保费分别为![]() 元,
元,![]() 元,
元,![]() 元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费![]() 、
、![]() 所要满足的条件;
所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业于保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择翻翻2的支出(不包括职工支出)低于选择方案1的支出期望,求保费![]() 、
、![]() 所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com