
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,且
,且![]() 为正三角形,
为正三角形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
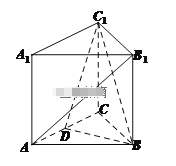
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)三棱柱![]() 的顶点都在一个球面上,求该球的体积.
的顶点都在一个球面上,求该球的体积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为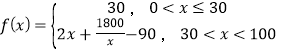 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 、
、![]() 、
、![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .
.

(1)若甲乙都以每分钟100![]() 的速度从点
的速度从点![]() 出发,甲沿
出发,甲沿![]() 运动,乙沿
运动,乙沿![]() 运动,乙比甲迟2分钟出发,求乙出发后的第1分钟末甲乙之间的距离;
运动,乙比甲迟2分钟出发,求乙出发后的第1分钟末甲乙之间的距离;
(2)现有甲、乙、丙三位小朋友分别在点![]() 、
、![]() 、
、![]() ,设
,设![]() ,乙丙之间的距离
,乙丙之间的距离![]() 是甲乙之间距离
是甲乙之间距离![]() 的2倍,且
的2倍,且![]() ,请将甲乙之间的距离
,请将甲乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲乙之间的最小距离.
的函数,并求甲乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,把
,把![]() 作为新数列
作为新数列![]() 的第一项,把
的第一项,把![]() 或
或![]() (
(![]() )作为新数列
)作为新数列![]() 的第
的第![]() 项,数列
项,数列![]() 称为数列
称为数列![]() 的一个生成数列.例如,数列
的一个生成数列.例如,数列![]() 的一个生成数列是
的一个生成数列是![]() .已知数列
.已知数列![]() 为数列
为数列![]() 的生成数列,
的生成数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)写出![]() 的所有可能值;
的所有可能值;
(2)若生成数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:对于给定的![]() ,
,![]() 的所有可能值组成的集合为
的所有可能值组成的集合为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,半径为
,半径为![]() .
.
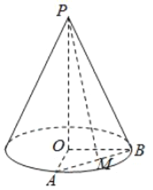
(1)设圆锥的母线长为![]() ,求圆锥的体积;
,求圆锥的体积;
(2)设![]() ,
,![]() 、
、![]() 是底面半径,且
是底面半径,且![]() ,
,![]() 为线段
为线段![]() 的中点,如图.求异面直线
的中点,如图.求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)判断点![]() 的位置,使得平面
的位置,使得平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com