练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f (x)有反函数，a是常数，那么方程f (x) = a的实根的状况是　　 (    )

    (A) 有且仅有一个实根      (B) 至少有一个实根

    (C) 至多有一个实根　　　　   (D) 至多有三个实根

     

    答案：C
    提示：

    有反函数的函数 x与y是一一对应的。

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黑龙江省龙东地区2011－2012学年度高二上学期高中教学联合体期末数学文科试卷 题型：044

    设函数f(x)＝x3＋x2＋(m2－1)x，(x∈R，)其中m＞0

    (1)当m＝1时，曲线y＝f(x)在点(1，f(1))处的切线方程

    (2)求函数的单调区间与极值；

    (3)已知函数f(x)有三个互不相同的零点0，x1，x2，且x1＜x2．若对任意的x∈[x1，x2]，f(x)＞f(1)恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)＝ x3－mx2＋(m2－4)x，x∈R．

    （1）当m＝3时，求曲线y＝f(x)在点（2，f(2)）处的切线方程；

    （2）已知函数f(x)有三个互不相同的零点0，α，β，且α＜β．若对任意的

    x∈[α，β]，都有f(x)≥f(1) 恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)＝－x3＋x2＋(a2－1)x，其中a>0.

    (1)若函数y＝f(x)在x＝－1处取得极值，求a的值；

    (2)已知函数f(x)有3个不同的零点，分别为0、x1、x2，且x1<x2，若对任意的x∈[x1，x2]，f(x)>f(1)恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：天津高考真题 题型：解答题

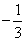    设函数f(x)=x3+x2+(m2-1)x(x∈R)，其中m＞0，
    (Ⅰ)当m=1时，求曲线y=f(x)在点(1，f(1))处的切线的斜率；
    (Ⅱ)求函数f(x)的单调区间与极值；
    (Ⅲ)已知函数f(x)有三个互不相同的零点0，x1，x2，且x1＜x2，若对任意的x∈[x1，x2]，f(x)＞f(1)恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：0103 期中题 题型：解答题

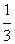    函数f(x)=x3-mx2+(m2-4)x，x∈R。
    （1）当m=3时，求曲线y=f(x)在点（2，f(2)）处的切线方程；
    （2）已知函数f(x)有三个互不相同的零点0，α ，β，且α＜β。若对任意的x∈[α ，β]，都有f(x)≥f(1)恒成立，求实数m的取值范围。

    查看答案和解析>>

    同步练习册答案