
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
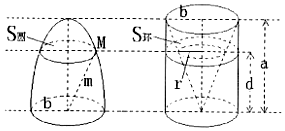 已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.
已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R+,使log2x0>0 | B. | 对任意的x∈R+,有log2x>0 | ||
| C. | 对任意的x∈R+,有log2x≤0 | D. | 存在x0∈R+,使log2x0>0 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:选择题
若函数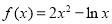 在其定义域的一个子区间
在其定义域的一个子区间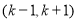 内不是单调函数,则实数
内不是单调函数,则实数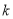 的取值范围是( )
的取值范围是( )
A.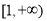 B.
B.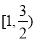 C.
C. D.
D.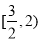
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com