
(Ⅰ)求x1、x2和xn的表达式;
(Ⅱ)求f(x)的表达式,并写出其定义域;
(Ⅲ)证明:y=f(x)的图象与y=x的图象没有横坐标大于1的交点.
(Ⅰ)解:依题意f(0)=0,又由f(x1)=1,当0≤y≤1时,函数y=f(x)的图象是斜率为b0=1的线段,
故由![]() =1得x1=1.
=1得x1=1.
又由f(x2)=2,当1≤y≤2时,函数y=f(x)的图象是斜率为b的线段,故由?
![]() =b,即x2-x1=
=b,即x2-x1=![]() 得x2=1+
得x2=1+![]() .记x0=0,
.记x0=0,
由函数y=f(x)图象中第n段线段的斜率为bn-1,故得?![]() =bn-1.?
=bn-1.?
又f(xn)=n, f(xn-1)=n-1;
∴xn-xn-1=(![]() )n-1,n=1,2,….?
)n-1,n=1,2,….?
由此知数列{xn-xn-1}为等比数列,其首项为1,公比为![]() .?
.?
因b≠1,得xn=![]() xk-xk-1)=1+
xk-xk-1)=1+![]() +…+
+…+![]() =
=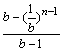 ,
,
即xn=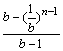 .
.
(Ⅱ)解:当0≤y≤1,从(Ⅰ)可知y=x,即当0≤x≤1时,f(x)=x.?
当n≤y≤n+1时,即当xn≤x≤xn+1时,由(Ⅰ)可知
f(x)=n+bn(x-xn)(xn≤x≤xn+1,n=1,2,3,…).
为求函数f(x)的定义域,须对xn=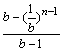 (n=1,2,3,…)进行讨论.??
(n=1,2,3,…)进行讨论.??
当b>1时,![]() xn=
xn=![]()
 =
=![]() ;?
;?
当0<b<1时,n→∞,xn也趋向于无穷大.
综上,当b>1时,y=f(x)的定义域为[0,![]() );?
);?
当0<b<1时,y=f(x)的定义域为[0,+∞).?
(Ⅲ)证法一:首先证明当b>1,1<x<![]() 时,恒有f(x)>x成立.
时,恒有f(x)>x成立.
用数学归纳法证明:?
(ⅰ)由(Ⅱ)知当n=1时,在(1,x2]上,y=f(x)=1+b(x-1),所以f(x)-x=(x-1)(b-1)>0成立?
(ⅱ)假设n=k时在(xk,xk+1]上恒有f(x)>x成立??
可得f(xk+1)=k+1>xk+1,?
在(xk+1,xk+2]上,f(x)=k+1+bk+1(x-xk+1),?
所以f(x)-x=k+1+bk+1(x-xk+1)-x=(bk+1-1)(x-xk+1)+(k+1-xk+1)>0成立.
由(ⅰ)与(ⅱ)知,对所有自然数n在(xn,xn+1]上都有f(x)>x成立.
即1<x<![]() 时,恒有f(x)>x.?
时,恒有f(x)>x.?
其次,当b<1,仿上述证明,可知当x>1时,恒有f(x)<x成立??
故函数y=f(x)的图象与y=x的图象没有横坐标大于1的交点??
证法二:首先证明当b>1,1<x<![]() 时,恒有f(x)>x成立??
时,恒有f(x)>x成立??
对任意的x∈(1,![]() ),存在xn,使xn<x≤xn+1?,?
),存在xn,使xn<x≤xn+1?,?
此时有f(x)-f(xn)=bn(x-xn)>x-x+n(n≥1),∴f(x)-x>f(xn)-xn.
又f(xn)=n>1+![]() +…+
+…+![]() =xn,∴f(xn)-xn>0,?
=xn,∴f(xn)-xn>0,?
∴f(x)-x>f(xn)-xn>0.?
即有f(x)>x成立?
其次,当b<1,仿上述证明,可知当x>1时,恒有f(x)<x成立.?
故函数f(x)的图象与y=x的图象没有横坐标大于1的交点.
评述:本小题主要考查函数的基本概念、等比数列、数列极限的基础知识,考查归纳、推理和综合的能力.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx |
| x |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com