
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为( )
甲 | 乙 | 原料限额 | |
A/吨 | 3 | 2 | 12 |
B/吨 | 1 | 2 | 8 |
A.15万元B.16万元C.17万元D.18万元
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】2021年某省将实行“![]() ”的新高考模式,即语文、数学、英语三科必选,物理、历史二选一,化学、生物、政治、地理四选二,若甲同学选科没有偏好,且不受其他因素影响,则甲同学同时选择历史和化学的概率为________
”的新高考模式,即语文、数学、英语三科必选,物理、历史二选一,化学、生物、政治、地理四选二,若甲同学选科没有偏好,且不受其他因素影响,则甲同学同时选择历史和化学的概率为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )
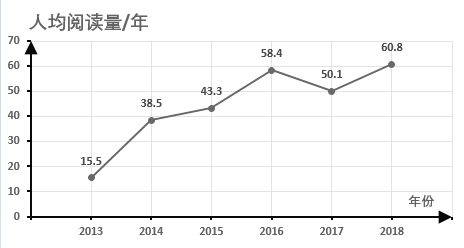
A.从2013年到2016年,该校纸质书人均阅读量逐年增长
B.2013年至2018年,该校纸质书人均阅读量的中位数是46.7本
C.2013年至2018年,该校纸质书人均阅读量的极差是45.3本
D.2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() 且渐近线为
且渐近线为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.曲线![]() 的方程为
的方程为![]() ;
;
B.左焦点到一条渐近线距离为![]() ;
;
C.直线![]() 与曲线
与曲线![]() 有两个公共点;
有两个公共点;
D.过右焦点截双曲线所得弦长为![]() 的直线只有三条;
的直线只有三条;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
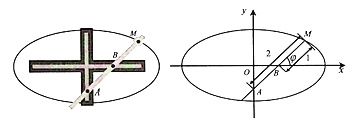
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com