
ΓΨΧβΡΩΓΩ“άΨίΡ≥ΒΊΡ≥ΧθΚ”Νς8‘¬ΖίΒΡΥ°ΈΡΙέ≤βΒψΒΡάζ ΖΆ≥ΦΤ ΐΨίΥυΜφ÷ΤΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΘ®ΦΉΘ©Υυ ΨΘΜ“άΨίΒ±ΒΊΒΡΒΊ÷ ΙΙ‘λΘ§ΒΟΒΫΥ°ΈΜ”κ‘÷ΚΠΒ»ΦΕΒΡΤΒ¬ Ζ÷≤ΦΧθ–ΈΆΦ»γΆΦΘ®““Θ©Υυ Ψ.
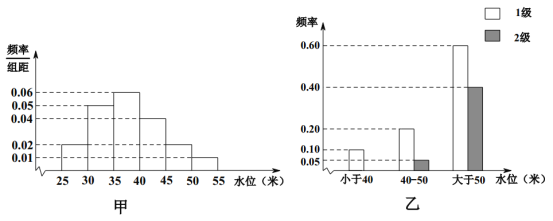
Θ®1Θ© ‘ΙάΦΤΗΟΚ”Νς‘Ύ8‘¬ΖίΥ°ΈΜΒΡ÷Ύ ΐΘΜ
Θ®2Θ©Έ“Ο«÷ΣΒά»τΗΟΚ”Νς8‘¬ΖίΒΡΥ°ΈΜ–Γ”Ύ40ΟΉΒΡΤΒ¬ ΈΣfΘ§ΗΟΚ”Νς8‘¬ΖίΒΡΥ°ΈΜ–Γ”Ύ40ΟΉΒΡ«ιΩωœ¬ΖΔ…ζ1ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣgΘ§‘ρΗΟΚ”Νς8‘¬ΖίΒΡΥ°ΈΜ–Γ”Ύ40«“ΖΔ…ζ1ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣ![]() Θ§ΤδΥϊ«ιΩωάύΥΤ.Ψί¥ΥΘ§ ‘Ζ÷±πΙάΦΤΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ12ΦΕ‘÷ΚΠΦΑ≤ΜΖΔ…ζ‘÷ΚΠΒΡΤΒ¬
Θ§ΤδΥϊ«ιΩωάύΥΤ.Ψί¥ΥΘ§ ‘Ζ÷±πΙάΦΤΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ12ΦΕ‘÷ΚΠΦΑ≤ΜΖΔ…ζ‘÷ΚΠΒΡΤΒ¬ ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©ΗΟΚ”Νς”ρΡ≥Τσ“ΒΘ§‘Ύ8‘¬ΖίΘ§»τΟΜ ή12ΦΕ‘÷ΚΠ”ΑœλΘ§άϊ»σΈΣ500Άρ‘ΣΘΜ»τ ή1ΦΕ‘÷ΚΠ”ΑœλΘ§‘ρΩςΥπ100Άρ‘ΣΘΜ»τ ή2ΦΕ‘÷ΚΠ”Αœλ‘ρΩςΥπ1000Άρ‘Σ.œ÷¥ΥΤσ“Β”–»γœ¬»ΐ÷÷”ΠΕ‘ΖΫΑΗ:
ΖΫΑΗ | ΖάΩΊΒ»ΦΕ | Ζ―”ΟΘ®ΒΞΈΜ:Άρ‘ΣΘ© |
ΖΫΑΗ“Μ | Έό¥κ © | 0 |
ΖΫΑΗΕΰ | ΖάΩΊ1ΦΕ‘÷ΚΠ | 40 |
ΖΫΑΗ»ΐ | ΖάΩΊ2ΦΕ‘÷ΚΠ | 100 |
‘Έ Θ§»γΫω¥”άϊ»σΩΦ¬«Θ§ΗΟΤσ“Β”Π―Γ‘ώ’β»ΐ÷÷ΖΫΑΗ÷–ΒΡΡΡ÷÷ΖΫΑΗ?ΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®1Θ©37.5Θ®2Θ©ΖΔ…ζ0.155Θ§ 0.035ΘΜ≤ΜΖΔ…ζ0.81Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±πΈΣ0.155Θ§0.035Θ§0.81Θ®3Θ©ΖΫΑΗΕΰΘ§άμ”…ΦϊΫβΈω
Ζ÷±πΈΣ0.155Θ§0.035Θ§0.81Θ®3Θ©ΖΫΑΗΕΰΘ§άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΉνΗΏΒΡΨΊ–ΈΒΡ÷–ΒψΦ¥ΈΣ÷Ύ ΐΘ§Φ¥Ω…ΒΟΒΫ±ΨΧβ¥πΑΗΘΜ
Θ®2Θ©”…ΦΉΆΦΘ§ΒΟΗΟΚ”Νς8‘¬ΖίΒΡΥ°ΈΜ–Γ”Ύ40ΟΉΘ§‘Ύ40ΟΉΚΆ50ΟΉ÷°ΦδΘ§¥σ”Ύ50ΟΉΒΡΕ‘”ΠΒΡΤΒ¬ Θ§ΫαΚœ““ΆΦΘ§Φ¥Ω…ΥψΒΟΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ1ΦΕ‘÷ΚΠΓΔ2ΦΕ‘÷ΚΠΚΆ≤ΜΖΔ…ζ‘÷ΚΠΒΡΕ‘”ΠΒΡΤΒ¬ ΘΜ
Θ®3Θ©Α―»ΐ÷÷ΖΫΑΗΕ‘”ΠΒΡΤΫΨυάϊ»σΥψ≥ωά¥Θ§±»Ϋœ¥σ–ΓΘ§Φ¥Ω…ΒΟΒΫ±ΨΧβ¥πΑΗ.
Θ®1Θ©”…ΧβΒΟΘ§![]() Θ§ΙάΦΤΗΟΚ”Νς‘Ύ8‘¬ΖίΥ°ΈΜΒΡ÷Ύ ΐΈΣ37.5ΟΉ
Θ§ΙάΦΤΗΟΚ”Νς‘Ύ8‘¬ΖίΥ°ΈΜΒΡ÷Ύ ΐΈΣ37.5ΟΉ
Θ®2Θ©“άΨίΦΉΆΦΘ§ΗΟΚ”Νς8‘¬ΖίΒΡΥ°ΈΜ–Γ”Ύ40ΟΉΘ§‘Ύ40ΟΉΚΆ50ΟΉ÷°ΦδΘ§¥σ”Ύ50ΟΉΒΡΤΒ¬ Ζ÷±πΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .ΗυΨί““ΆΦΘ§ΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ1ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣ
.ΗυΨί““ΆΦΘ§ΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ1ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣ![]() ΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ2ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣ
ΗΟΚ”Νς‘Ύ8‘¬ΖίΖΔ…ζ2ΦΕ‘÷ΚΠΒΡΤΒ¬ ΈΣ![]() ΗΟΚ”Νς‘Ύ8‘¬Ζί≤ΜΖΔ…ζ‘÷ΚΠΒΡΤΒ¬ ΈΣ
ΗΟΚ”Νς‘Ύ8‘¬Ζί≤ΜΖΔ…ζ‘÷ΚΠΒΡΤΒ¬ ΈΣ![]() ΙάΦΤ
ΙάΦΤ![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±πΈΣ0.155Θ§0.035Θ§0.81.
Ζ÷±πΈΣ0.155Θ§0.035Θ§0.81.
Θ®3Θ©”…Θ®2Θ©»τ―Γ‘ώΖΫΑΗ“ΜΘ§‘ρΗΟΤσ“Β‘Ύ8‘¬ΖίΒΡΤΫΨυάϊ»σ![]() Θ®Άρ‘ΣΘ©;
Θ®Άρ‘ΣΘ©;
»τ―Γ‘ώΖΫΑΗΕΰΘ§‘ρΗΟΤσ“Β‘Ύ8‘¬ΖίΒΡΤΫΨυάϊ»σ![]() Θ®Άρ‘ΣΘ©ΘΜ
Θ®Άρ‘ΣΘ©ΘΜ
»τ―Γ‘ώΖΫΑΗ»ΐΘ§‘ρΗΟΤσ“Β‘Ύ8‘¬ΖίΒΡΤΫΨυάϊ»σ![]() Θ®Άρ‘ΣΘ©.
Θ®Άρ‘ΣΘ©.
”…”Ύ![]() Θ§“ρ¥ΥΤσ“Β”Π―ΓΖΫΑΗΕΰ
Θ§“ρ¥ΥΤσ“Β”Π―ΓΖΫΑΗΕΰ



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύάβ≥ΛΈΣaΒΡ’ΐΖΫΧεABCD©¹A1B1C1D1÷–Θ§PΘ§QΘ§LΖ÷±πΈΣάβA1D1Θ§C1D1Θ§BCΒΡ÷–ΒψΘ°
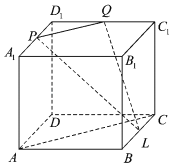
Θ®1Θ©«σ÷ΛΘΚACΓΆQLΘΜ
Θ®2Θ©«σΥΡΟφΧεDPQLΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®
Θ®![]() Θ©.
Θ©.
Θ®ΔώΘ©…η![]() ΈΣΚ· ΐ
ΈΣΚ· ΐ![]() ΒΡΒΦΚ· ΐΘ§«σΚ· ΐ
ΒΡΒΦΚ· ΐΘ§«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®ΔρΘ©»τΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œ”–Ήν¥σ÷ΒΘ§«σ Β ΐ
…œ”–Ήν¥σ÷ΒΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΆ÷‘≤![]() (
(![]() )ΒΡ“ΜΗωΫΙΒψ
)ΒΡ“ΜΗωΫΙΒψ![]() Βψ
Βψ![]() ΈΣΆ÷‘≤
ΈΣΆ÷‘≤![]() ΡΎ“ΜΒψ,»τΆ÷‘≤
ΡΎ“ΜΒψ,»τΆ÷‘≤![]() …œ¥φ‘Ύ“ΜΒψ
…œ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ§‘ρΆ÷‘≤
Θ§‘ρΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
ΒΡάκ–Ρ¬ ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ‘ΎΕ®“ε”ρΡΎ”–ΝΫΗω≤ΜΆ§ΒΡΦΪ÷ΒΒψ.
‘ΎΕ®“ε”ρΡΎ”–ΝΫΗω≤ΜΆ§ΒΡΦΪ÷ΒΒψ.
Θ®ΔώΘ©«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®ΔρΘ©Φ«ΝΫΗωΦΪ÷ΒΒψΈΣ![]() Θ§«“
Θ§«“![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() «‘≤÷υ
«‘≤÷υ![]() ΒΉΟφ‘≤OΒΡ÷±ΨΕΘ§ΒΉΟφΑκΨΕ
ΒΉΟφ‘≤OΒΡ÷±ΨΕΘ§ΒΉΟφΑκΨΕ![]() Θ§‘≤÷υΒΡ±μΟφΜΐΈΣ
Θ§‘≤÷υΒΡ±μΟφΜΐΈΣ![]() Θ§Βψ
Θ§Βψ![]() ‘ΎΒΉΟφ‘≤
‘ΎΒΉΟφ‘≤![]() …œΘ§«“÷±œΏ
…œΘ§«“÷±œΏ![]() ”κœ¬ΒΉΟφΥυ≥…ΒΡΫ«ΒΡ¥σ–ΓΈΣ
”κœ¬ΒΉΟφΥυ≥…ΒΡΫ«ΒΡ¥σ–ΓΈΣ![]() .
.
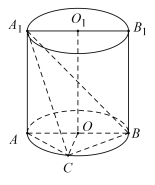
(1)«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
(2)«σΕΰΟφΫ«![]() ΒΡ¥σ–ΓΒΡ”ύœ“÷Β.
ΒΡ¥σ–ΓΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ΒΡΆΦœσ”κΙΐ‘≠ΒψΒΡ÷±œΏ«Γ”–ΥΡΗωΫΜΒψΘ§…ηΥΡΗωΫΜΒψ÷–ΚαΉχ±ξΉν¥σ÷ΒΈΣ
ΒΡΆΦœσ”κΙΐ‘≠ΒψΒΡ÷±œΏ«Γ”–ΥΡΗωΫΜΒψΘ§…ηΥΡΗωΫΜΒψ÷–ΚαΉχ±ξΉν¥σ÷ΒΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() Θ® Θ©
Θ® Θ©
A. ![]() B.
B. ![]() C. 0 D. 2
C. 0 D. 2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΘΫ|2x©¹1|©¹aΘ°
Θ®1Θ©Β±aΘΫ1 ±Θ§Ϋβ≤ΜΒ» ΫfΘ®xΘ©ΘΨx+1ΘΜ
Θ®2Θ©»τ¥φ‘Ύ Β ΐxΘ§ ΙΒΟfΘ®xΘ©![]() fΘ®x+1Θ©Θ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
fΘ®x+1Θ©Θ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪΚ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() ΡΎΒΡ»Ϊ≤ΩΦΪ÷ΒΒψΑ¥¥”–ΓΒΫ¥σΒΡΥ≥–ρ≈≈≥… ΐΝ–
ΡΎΒΡ»Ϊ≤ΩΦΪ÷ΒΒψΑ¥¥”–ΓΒΫ¥σΒΡΥ≥–ρ≈≈≥… ΐΝ–![]() Θ°
Θ°
Θ®1Θ©«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…η![]() Θ§ ΐΝ–
Θ§ ΐΝ–![]() ΒΡ«ΑnœνΚΆ
ΒΡ«ΑnœνΚΆ![]() Θ§«σ÷ΛΘΚ ΐΝ–
Θ§«σ÷ΛΘΚ ΐΝ–![]() ΈΣΒ»±» ΐΝ–Θ§≤Δ«σ
ΈΣΒ»±» ΐΝ–Θ§≤Δ«σ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com