练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图,已知三棱柱的底面是边长为2的正三角形,侧棱与下底面相邻的两边AB,AC均成45度的角.

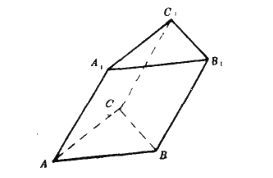
    (1)求点到平面B1BCC1的距离.

    (2)试问,当为多长时,点到平面与到平面的距离相等.

    【答案】(1) (2)

    【解析】

    设BC,B1C1中点为D,D1.

    (1) 因为侧棱与下底面相邻的两边AB,AC均成45度的角，所以点在底面的投影O在∠BAC角平分线AD上，由三垂线定理得侧棱垂直BC,所以过点作DD1垂线于E点，则为点到平面B1BCC1的距离.

    由三余弦定理得cos∠BACcos300=cos450, cos∠BAC=,

    从而点到平面B1BCC1的距离为A1D1sin∠BAC=,

    (2)因为点到平面与到平面的距离相等，所以A1A=A1D1= .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业（以下简称外卖甲，外卖乙）的经营情况进行了调查，调查结果如表：

    1日

    2日

    3日

    4日

    5日

    外卖甲日接单（百单）

    5

    2

    9

    8

    11

    外卖乙日接单（百单）

    2.2

    2.3

    10

    5

    15

    （1）据统计表明，与之间具有线性相关关系.

    （ⅰ）请用相关系数加以说明：（若，则可认为与有较强的线性相关关系（值精确到0.001））

    （ⅱ）经计算求得与之间的回归方程为.假定每单外卖业务企业平均能获纯利润3元，试预测当外卖乙日接单量不低于2500单时，外卖甲所获取的日纯利润的大致范围：（值精确到0.01）

    （2）试根据表格中这五天的日接单量情况，从平均值和方差角度说明这两家外卖企业的经营状况.

    相关公式：相关系数，

    参考数据：

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直角梯形与等腰直角三角形所在的平面互相垂直. ,，.

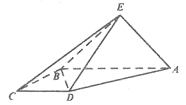
    （1）求证：；

    （2）求证：平面平面；

    （3）线段上是否存在点，使平面？若存在，求出的值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面内有12个点，其中任意三点不共线，每两点连一条线段（或边）。这些线段用红、蓝两色染色，每条线段恰染一色，其中，从某点出发的红色线段有奇数条，而从其余11个点出发的红色线段数互不相同。求以已知点为顶点、各边均为红色的三角形个数及两边为红色、另一边为蓝色的三角形个数。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象在点处的切线方程为.

    （1）求函数的解析式；

    （2）若对任意，不等式恒成立，求正整数t的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】空气质量指数(Air Quality Index，简称AQI)是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；>300为严重污染.一环保人士记录了某地2020年某月10天的AQI的茎叶图如图所示.

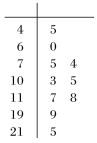
    （1）利用该样本估计该地本月空气质量优良(AQI≤100)的天数；(按这个月总共有30天计算)

    （2）若从样本中的空气质量不佳(AQI>100)的这些天中，随机地抽取两天深入分析各种污染指标，求该两天的空气质量等级恰好不同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

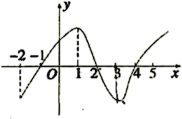
    【题目】如图是的导函数的图象，对于下列四个判断，其中正确的判断是（ ）.

    A.在上是增函数；

    B.当时，取得极小值；

    C.在上是增函数、在上是减函数；

    D.当时，取得极大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业有，两个分厂生产某种产品，规定该产品的某项质量指标值不低于130的为优质品．分别从，两厂中各随机抽取100件产品统计其质量指标值，得到如图频率分布直方图：

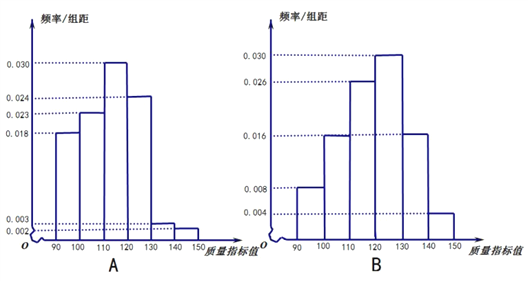
    （1）根据频率分布直方图，分别求出分厂的质量指标值的众数和中位数的估计值；

    （2）填写列联表，并根据列联表判断是否有的把握认为这两个分厂的产品质量有差异？

    优质品

    非优质品

    合计

    合计

    （3）（i）从分厂所抽取的100件产品中，利用分层抽样的方法抽取10件产品，再从这10件产品中随机抽取2件，已知抽到一件产品是优质品的条件下，求抽取的两件产品都是优质品的概率；

    （ii）将频率视为概率，从分厂中随机抽取10件该产品，记抽到优质品的件数为，求的数学期望．

    附：

    0.100

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近日，据媒体报道称，“杂交水稻之父”袁隆平及其团队培育的超级杂交稻品种“湘两优900（超优千号）”再创亩产世界纪录，经第三方专家测产，该品种的水稻在实验田内亩产1203.36公斤.中国工程院院士袁隆平在1973年率领科研团队开启了的杂交水稻王国的大门，在数年的时间内就解决了十多亿人的吃饭问题，有力回答了世界“谁来养活中国”的疑问.2012年，在袁隆平的实验田内种植了，两个品种的水稻，为了筛选出更优的品种，在，两个品种的实验田中分别抽取7块实验田，如图所示的茎叶图记录了这14块实验田的亩产量（单位：），通过茎叶图比较两个品种的均值及方差，并从中挑选一个品种进行以后的推广，有如下结论：①.品种水稻的平均产量高于品种水稻，推广品种水稻；②.品种水稻的平均产量高于品种水稻，推广品种水稻；③.品种水稻的比品种水稻产量更稳定，推广品种水稻；④.品种水稻的比品种水稻产量更稳定，推广品种水稻；

    其中正确结论的编号为（ ）

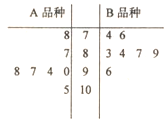
    A. ①② B. ①③ C. ②④ D. ①④

    查看答案和解析>>

    同步练习册答案