
(本题满分14分)如图,在四棱锥P-ABCD中,PA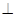 底面ABCD,
底面ABCD,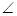 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
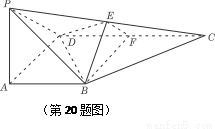
(Ⅰ)试证:CD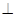 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于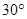 ,求k的取值范围.
,求k的取值范围.
(Ⅰ)见解析;(Ⅱ)k的取值范围为k>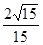
【解析】本试题主要考查了立体几何中线面的垂直的证明以及二面角的求解的综合运用
(1)根据已知的条件,通过线线垂直来判定函数的线面垂直的证明。即由已知DF∥AB且 DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD BF.
BF.
又PA 底面ABCD,CD
底面ABCD,CD AD,故知CD
AD,故知CD PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD EF,由此得CD
EF,由此得CD 面BEF.
面BEF.
(2)建立合理的空间直角坐标系来表示空间向量的坐标,然后求解法向量,运用法向量的夹角来表示二面角的平面角的大小。
(Ⅰ)解法一:
(Ⅰ)证:由已知DF∥AB且 DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD BF.
………..4分
BF.
………..4分
又PA 底面ABCD,CD
底面ABCD,CD AD,故知CD
AD,故知CD PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD EF,由此得CD
EF,由此得CD 面BEF. ………..7分
面BEF. ………..7分
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,
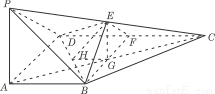
则在△PAC中易知EC∥PA.又因
PA 底面ABCD,故BC
底面ABCD,故BC 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH BD.从而
BD.从而 EHG为二面角E-BD-C的平面角. ………..10分
EHG为二面角E-BD-C的平面角. ………..10分
设AB=a,则在△PAC中,有
BG=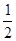 PA=
PA=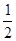 ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.

因S△CBD=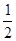 BD·GH=
BD·GH=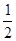 GB·OF.故GH=
GB·OF.故GH=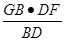 .
.
在△ABD中,因为AB=a,AD=2A,得BD=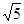 a
a
而GB=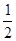 FB=
FB=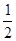 AD-a.DF-AB,从而得GH=
AD-a.DF-AB,从而得GH=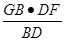 =
=
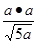 =
=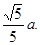 因此tanEHG=
因此tanEHG= =
=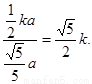 ………..12分
………..12分
由k>0知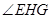 是锐角,故要使
是锐角,故要使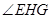 >
>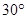 ,必须
,必须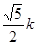 >tan
>tan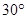 =
=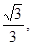
解之得,k的取值范围为k>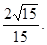 ………..14分
………..14分
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),F(a,2a,0).
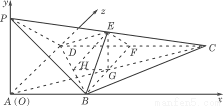
从而 =(2a,0,0),
=(2a,0,0), 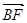 =(0,2a,0),
=(0,2a,0),
 ·
·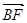 =0,故
=0,故

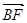
设PA=b,则P(0,0,b),而E为PC中点.故
E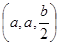 .从而
.从而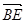 =
=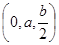 .
.  ·
·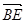 =0,故
=0,故

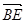 .
.
由此得CD 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH BD.
BD.
从而 EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E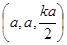 ,G(a,a,0).设H(x,y,0),则
,G(a,a,0).设H(x,y,0),则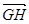 =(x-a,y-a,0),
=(x-a,y-a,0), 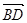 =(-a,2a,0),
=(-a,2a,0),
由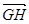 ·
·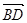 =0得=a(x-a)+2a(y-a)=0,即x-2y=-a
①
=0得=a(x-a)+2a(y-a)=0,即x-2y=-a
①
又因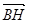 =(x,a,y,0),且
=(x,a,y,0),且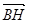 与
与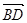 的方向相同,故
的方向相同,故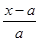 =
= ,即2x+y=2a ②
,即2x+y=2a ②
由①②解得x=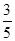 a,y=
a,y=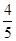 a,从而
a,从而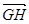 =
= ,|
,|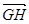 |=
|=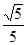 a.
a.
tanEHG=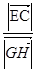 =
=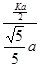 =
=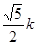 .由k>0知,EHC是锐角,由
.由k>0知,EHC是锐角,由 EHC>
EHC>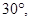 得tanEHG>tan
得tanEHG>tan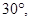 即
即
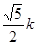 >
>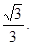 故k的取值范围为k>
故k的取值范围为k>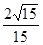


科目:高中数学 来源: 题型:
(本题满分14分)如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图,已知直三棱柱ABC—A1B1C1,![]() ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,![]()
(1)求证:![]() ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.

(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
(本题满分14分)如图,正方形 、
、 的边长都是1,平面
的边长都是1,平面
 平面
平面 ,点
,点 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)

(I)求 的长;
的长;
(II) 为何值时,
为何值时, 的长最小;
的长最小;
(III)当 的长最小时,求面
的长最小时,求面 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
查看答案和解析>>
科目:高中数学 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分14分)如图,矩形BCC1B1所在平面垂直于三角形ABC所在平面,BB1=CC1=AC=2, ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。
 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com