练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求两个向量和向量的运算
    求两个向量和向量的运算
    叫向量的加法．从几何上看，求向量加法常借助于两个图形，分别是
    三角形
    三角形
    和
    平行四边形
    平行四边形
    ；与这两个图形相对应向量加法称为
    三角形
    三角形
    法则和
    平行四边形
    平行四边形
    法则．
    分析：由向量加法的定义，及向量加法的几何意义，我们易得答案．
    解答：解：根据向量加法的定义我们可得：
    求两个向量和向量的运算叫向量的加法，
    计算时常借助于三角形和平行四边形，
    对应的向量加法称为三角形法则和平行四边形法则．
    故答案为：求两个向量和向量的运算，三角形，平行四边形，三角形，平行四边形．
    点评：本题考查的知识点向量的加法及其几何意义，熟练掌握向量加法的定义及其几何意义是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某教授为了测试贫困地区和发达地区的同龄儿童的智力，出了10个智力题，每个题10分，然后作了统计，结果如图：
    精英家教网
    （1）完成上面的表格；
    （2）求两个地区参加测试的儿童得60分以上的概率；
    （3）分析贫富差距为什么会带来人的智力的差别、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某教授为了测试贫困地区和发达地区的同龄儿童的智力,出了10个智力题,每个题10分,然后作了统计,下表是统计结果：

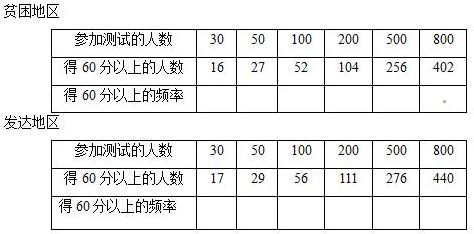
    贫困地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    16

    27

    52

    104

    256

    402

    得60分以上的频率

     

     

     

     

     

     

    发达地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    17

    29

    56

    111

    276

    440

    得60分以上的频率

     

     

     

     

     

     

    （1）利用计算器计算两地区参加测试的儿童中得60分以上的频率;

    （2）求两个地区参加测试的儿童得60分以上的概率;

    （3）分析贫富差距为什么会带来人的智力的差别.

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学必修3 3.1随机事件及其概率练习卷（解析版）） 题型：解答题

    某教授为了测试贫困地区和发达地区的同龄儿童的智力，出了10个智力题，每个题10分，然后作了统计，结果如下：

     

     

    贫困地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    16

    27

    52

    104

    256

    402

    得60分以上的频率

     

     

     

     

     

     

    发达地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    17

    29

    56

    111

    276

    440

    得60分以上的频率

     

     

     

     

     

     

    （1）计算两地区参加测试的儿童得60分以上的频率；

    （2）求两个地区参加测试的儿童得60分以上的概率；

    （3）分析贫富差距为什么会带来人的智力的差别．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某教授为了测试贫困地区和发达地区的同龄儿童的智力，出了10个智力题，每个题10分.然后作了统计，下表是统计结果.

    贫困地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    16

    27

    52

    104

    256

    402

    得60分以上的频率

     

     

     

     

     

     

    发达地区

    参加测试的人数

    30

    50

    100

    200

    500

    800

    得60分以上的人数

    17

    29

    56

    111

    276

    440

    得60分以上的频率

     

     

     

     

     

     

    （1）利用计算器计算两地区参加测试的儿童中得60分以上的频率；

    （2）求两个地区参加测试的儿童得60分以上的概率；

    （3）分析贫富差距为什么会带来人的智力的差别.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个袋子中装有m个红球和n个白球(m＞n≥4),它们除颜色不同外,其余都相同,现从中任取两个球.

    (1)若取出两个红球的概率等于取出一红一白两个球的概率的整数倍,求证:m必为奇数;

    (2)若取出两个球颜色相同的概率等于取出两个球颜色不同的概率,求满足m+n≤20的所有数组(m,n).

    查看答案和解析>>

    同步练习册答案