
分析 (I)对任意n∈N*,满足an+1=an+can2(c>0且为常数).可得a2=${a}_{1}+c{a}_{1}^{2}$.a3=${a}_{2}+c{a}_{2}^{2}$.根据a1,2a2,3a3依次成等比数列,可得$(2{a}_{2})^{2}$=a1•3a3,a2>0,代入化为4a2=3a1(1+ca2).再代入化简解出即可得出.
(II)(i)由an+1=an+can2(c>0且为常数),an>0.代入$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}+c{a}_{n}^{2}}$-$\frac{1}{{a}_{n}}$.化简整理即可证明.
(ii)由(i)可得:$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-$\frac{c}{1+c{a}_{n}}$.bn=$\frac{1}{1+c{a}_{n}}$=$\frac{1}{c}$$(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$,利用“累加求和“方法可得Sn,再利用单调性即可证明.
解答 (I)解:对任意n∈N*,满足an+1=an+can2(c>0且为常数).∴a2=${a}_{1}+c{a}_{1}^{2}$.a3=${a}_{2}+c{a}_{2}^{2}$.
∵a1,2a2,3a3依次成等比数列,∴$(2{a}_{2})^{2}$=a1•3a3,∴$4{a}_{2}^{2}$=a1•3(${a}_{2}+c{a}_{2}^{2}$),a2>0,化为4a2=3a1(1+ca2).
∴4(${a}_{1}+c{a}_{1}^{2}$)=3a1[1+c(${a}_{1}+c{a}_{1}^{2}$)],a1>0,化为:3c2x2-cx-1=0,解得x=$\frac{1+\sqrt{13}}{6c}$.
(II)证明:(i)由an+1=an+can2(c>0且为常数),an>0.
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}+c{a}_{n}^{2}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}}(\frac{1}{1+c{a}_{n}}-1)$=-$\frac{c}{1+c{a}_{n}}$.即$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-$\frac{c}{1+c{a}_{n}}$.
(ii)由(i)可得:$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-$\frac{c}{1+c{a}_{n}}$.
∴bn=$\frac{1}{1+c{a}_{n}}$=$\frac{1}{c}$$(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$,
∴Sn=$\frac{1}{c}$$[(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}})+(\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}})$+…+$(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})]$=$\frac{1}{c}$$(\frac{1}{{a}_{1}}-\frac{1}{{a}_{n+1}})$.
由an+1=an+can2>an>0,可得-$\frac{1}{{a}_{n+1}}$$<-\frac{1}{{a}_{n+2}}$.
∴Sn<$\frac{1}{c}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{n+2}})$=Sn+1<$\frac{1}{c{a}_{1}}$.
∴Sn<Sn+1<$\frac{1}{c{a}_{1}}$.
点评 本题考查了数列递推关系、数列的单调性、“累加求和”方法、方程的解法、不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
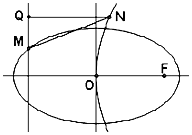 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}+3}}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}+$1 | C. | $\sqrt{7}$-1 | D. | 2$\sqrt{7}$-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com