
对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:
||AB||=|x2-x1|+|y2-y1|.
给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.
其中真命题的个数为
A.0
B.1
C.2
D.3
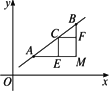
如图所示,所谓的距离||AB||=|x2-x1|+|y2-y1|,即以AB为斜边的直角三角形的两条直角边|AM|与|BM|之和.(若AB与坐标轴平行,则与线段|AB|的距离概念相同).若点C在线段AB上,则||AC||+||CB||=|AE|+|EC|+|CF|+|FB|=|AM|+|MB|=||AB||;即得命题①正确;
△ABC中,若∠C=90°,则||AB||2=(||AC||+||CB||)2=||AC||2+||CB||2+2||AC||||CB||>||AC||2+||CB||2,即命题②不正确;
显然在Rt△ABC中,若∠C=90°,有||AB||=||AC||+||CB||,即命题③不正确,故应选B.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知θ∈[0,
(2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知θ∈[0,| π |
| 3 |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年福建省高二第二学期半期考试数学(理科)试题 题型:选择题
对于直角坐标平面内的任意两点A(x ,
, y
y )、B(x
)、B(x ,y
,y ),定义它们之间的一种“距离”:
),定义它们之间的一种“距离”:
‖AB‖=︱x -x
-x ︱+︱y
︱+︱y -y
-y ︱。给出下列三个命题:
︱。给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖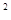 +‖CB‖
+‖CB‖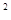 =‖AB‖
=‖AB‖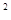 ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com