
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设 ![]() 为等差数列
为等差数列 ![]() 的前
的前 ![]() 项和,其中
项和,其中 ![]() ,且
,且 ![]() .
.
(1)求常数 ![]() 的值,并写出
的值,并写出 ![]() 的通项公式;
的通项公式;
(2)记 ![]() ,数列
,数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,若对任意的
,若对任意的 ![]() ,都有
,都有 ![]() ,求常数
,求常数 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 的顶点在原点
的顶点在原点 ![]() ,对称轴是
,对称轴是 ![]() 轴,且过点
轴,且过点 ![]() .
.
(Ⅰ)求抛物线 ![]() 的方程;
的方程;
(Ⅱ)已知斜率为 ![]() 的直线
的直线 ![]() 交
交 ![]() 轴于点
轴于点 ![]() ,且与曲线
,且与曲线 ![]() 相切于点
相切于点 ![]() ,点
,点 ![]() 在曲线
在曲线 ![]() 上,且直线
上,且直线 ![]() 轴,
轴, ![]() 关于点
关于点 ![]() 的对称点为
的对称点为 ![]() ,判断点
,判断点 ![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
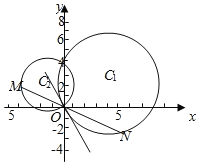
【题目】已知圆![]() 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图)如果小正方形的边长为1,大正方形的边长为5,直角三角形中较小的锐角为![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中
,其中 ![]() ,则
,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2,3+ ![]() ]
]
B.[2,3+ ![]() ]
]
C.[3- ![]() , 3+
, 3+ ![]() ]
]
D.[3- ![]() , 3+
, 3+ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com