
°æƒø°øπ≤œÌµ•≥µΩ¯◊§≥« –£¨¬Ã…´≥ˆ––“˝¡Ï ±…–.ƒ≥ –”–Õ≥º∆ ˝æ𜑠棨2017ƒÍ∏√ –π≤œÌµ•≥µ”√ªßƒÍ¡‰µ«º«∑÷≤º»ÁÕº1À˘ 棨“ª÷Ѓ⁄ –√Ò π”√µ•≥µµƒ∆µ¬ ∑÷≤º…»–ŒÕº»ÁÕº2À˘ æ.»ÙΩ´π≤œÌµ•≥µ”√ªß∞¥’’ƒÍ¡‰∑÷Œ™°∞ƒÍ«·»À°±£®20ÀÍ÷¡39ÀÍ£©∫Õ°∞∑«ƒÍ«·»À°±£®19Àͺ∞“‘œ¬ªÚ’þ40Àͺ∞“‘…œ£©¡Ω¿ý£¨Ω´“ª÷Ѓ⁄ π”√µƒ¥Œ ˝Œ™6¥ŒªÚ6¥Œ“‘…œµƒ≥∆Œ™°∞æ≠≥£ π”√µ•≥µ”√ªß°±£¨ π”√¥Œ ˝Œ™5¥ŒªÚ≤ª◊„5¥Œµƒ≥∆Œ™°∞≤ª≥£ π”√µ•≥µ”√ªß°±£Æ“—÷™‘⁄°∞æ≠≥£ π”√µ•≥µ”√ªß°±÷–”–![]() «°∞ƒÍ«·»À°±£Æ
«°∞ƒÍ«·»À°±£Æ
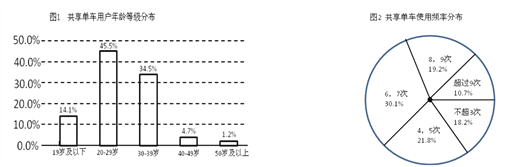
£®1£©œ÷∂‘∏√ – –√ÒΩ¯––°∞æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰πÿœµ°±µƒµ˜≤È£¨≤…”√Àʪ˙≥È—˘µƒ∑Ω∑®£¨≥È»°“ª∏ˆ»ð¡øŒ™200µƒ—˘±æ£¨«Îƒ„∏˘æðÕº±Ì÷–µƒ ˝æð£¨≤π»´œ¬¡–![]() ¡–¡™±Ì£¨≤¢∏˘æð¡–¡™±Ìµƒ∂¿¡¢–‘ºÏ—È£¨≈–∂œƒÐ”–∂ý¥Û∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ£ø
¡–¡™±Ì£¨≤¢∏˘æð¡–¡™±Ìµƒ∂¿¡¢–‘ºÏ—È£¨≈–∂œƒÐ”–∂ý¥Û∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ£ø

£®2£©Ω´∆µ¬ ”Œ™∏≈¬ £¨»Ù¥”∏√ – –√Ò÷–Àʪ˙»Œ»°3»À£¨…Ë∆‰÷–æ≠≥£ π”√π≤œÌµ•≥µµƒ°∞∑«ƒÍ«·»À°±»À ˝Œ™Àʪ˙±‰¡ø![]() £¨«Û
£¨«Û![]() µƒ∑÷≤º”Î∆⁄Õ˚.
µƒ∑÷≤º”Î∆⁄Õ˚.
£®≤Œøº ˝æð£∫∂¿¡¢–‘ºÏ—ÈΩÁ÷µ±Ì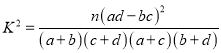 £¨∆‰÷–
£¨∆‰÷–![]() £©
£©

°æ¥∞∏°ø(1) ”–85%µƒ∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ;(2)º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æðπ≤œÌµ•≥µ”√ªßƒÍ¡‰µ»º€∑÷≤º±Ì÷– ˝æð£¨ø…≤π»´œ¬¡–![]() ¡–¡™±Ì£¨¿˚”√π´ Ωø…µ√
¡–¡™±Ì£¨¿˚”√π´ Ωø…µ√![]()
![]() £¨¥”∂¯ø…µ√”–85%µƒ∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ£ª£®2£©
£¨¥”∂¯ø…µ√”–85%µƒ∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ£ª£®2£©![]() µƒø…ƒÐ»°÷µŒ™
µƒø…ƒÐ»°÷µŒ™![]() £¨∏˘æð∂¿¡¢ ¬º˛∏≈¬ π´ Ω«Û≥ˆ∏˜Àʪ˙±‰¡ø∂‘”¶µƒ∏≈¬ £¨¥”∂¯ø…µ√∑÷≤º¡–£¨Ω¯∂¯¿˚”√∆⁄Õ˚π´ Ωø…µ√
£¨∏˘æð∂¿¡¢ ¬º˛∏≈¬ π´ Ω«Û≥ˆ∏˜Àʪ˙±‰¡ø∂‘”¶µƒ∏≈¬ £¨¥”∂¯ø…µ√∑÷≤º¡–£¨Ω¯∂¯¿˚”√∆⁄Õ˚π´ Ωø…µ√![]() µƒ ˝—ß∆⁄Õ˚..
µƒ ˝—ß∆⁄Õ˚..
‘Ã‚Ω‚Œˆ£∫£®1£©≤π»´µƒ¡–¡™±Ì»Áœ¬£∫
ƒÍ«·»À | ∑«ƒÍ«·»À | ∫œº∆ | |
æ≠≥£ π”√π≤œÌµ•≥µ | 100 | 20 | 120 |
≤ª≥£ π”√π≤œÌµ•≥µ | 60 | 20 | 80 |
∫œº∆ | 160 | 40 | 200 |
”⁄ «![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨
°ý![]()
![]() £¨
£¨
º¥”–85%µƒ∞—Œ’ø…“‘»œŒ™æ≠≥£ π”√π≤œÌµ•≥µ”΃͡‰”–πÿ.
£®2£©”…£®1£©µƒ¡–¡™±Ìø…÷™£¨æ≠≥£ π”√π≤œÌµ•≥µµƒ°∞∑«ƒÍ«·»À°±’º—˘±æ◊Ð ˝µƒ∆µ¬ Œ™![]() £¨º¥‘⁄≥È»°µƒ”√ªß÷–≥ˆœ÷æ≠≥£ π”√µ•≥µµƒ°∞∑«ƒÍ«·»À°±µƒ∏≈¬ Œ™0.1£¨
£¨º¥‘⁄≥È»°µƒ”√ªß÷–≥ˆœ÷æ≠≥£ π”√µ•≥µµƒ°∞∑«ƒÍ«·»À°±µƒ∏≈¬ Œ™0.1£¨
°ý![]() £¨
£¨ ![]()
![]()
![]() £¨
£¨
°ý![]() µƒ∑÷≤º¡–Œ™
µƒ∑÷≤º¡–Œ™
| 0 | 1 | 2 | 3 |
| 0.729 | 0.243 | 0.027 | 0.001 |
°ý![]() µƒ ˝—ß∆⁄Õ˚
µƒ ˝—ß∆⁄Õ˚![]()


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂®µ„![]() £¨
£¨ ![]() Œ™‘≤
Œ™‘≤![]() …œ»Œ“‚“ªµ„£¨œþ∂Œ
…œ»Œ“‚“ªµ„£¨œþ∂Œ![]() …œ“ªµ„
…œ“ªµ„![]() ¬˙◊„
¬˙◊„![]() £¨÷±œþ
£¨÷±œþ![]() …œ“ªµ„
…œ“ªµ„![]() £¨¬˙◊„
£¨¬˙◊„![]() .
.
£®1£©µ±![]() ‘⁄‘≤÷Ð…œ‘À∂Ø ±£¨«Ûµ„
‘⁄‘≤÷Ð…œ‘À∂Ø ±£¨«Ûµ„![]() µƒπϺ£
µƒπϺ£![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©»Ù÷±œþ![]() ”Ϋ˙œþ
”Ϋ˙œþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨«““‘
¡Ωµ„£¨«““‘![]() Œ™÷±æ∂µƒ‘≤π˝‘≠µ„
Œ™÷±æ∂µƒ‘≤π˝‘≠µ„![]() £¨«Û÷§£∫÷±œþ
£¨«Û÷§£∫÷±œþ![]() ”Î
”Î![]() ≤ªø…ƒÐœý«–.
≤ªø…ƒÐœý«–.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™∂‘ƒœøµ«¯∫Õ”⁄∂ºœÿ¡Ω«¯œÿƒ≥¥Œ¡™øº≥…º®Ω¯––∑÷Œˆ£¨Àʪ˙≥È≤È¡À¡Ωµÿ“ªπ≤10000√˚øº…˙µƒ≥…º®£¨∏˘æðÀ˘µ√ ˝æðª≠¡À»Áœ¬µƒ—˘±æ∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ
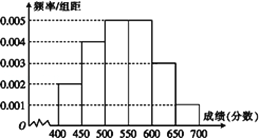
(1)«Û≥…º®‘⁄![]() µƒ∆µ¬ £ª
µƒ∆µ¬ £ª
(2)∏˘æð∆µ¬ ∑÷≤º÷±∑ΩÕºÀ„≥ˆ—˘±æ ˝æð∆Ωæ˘ ˝£ª
(3)Œ™¡À∑÷Œˆ≥…º®”Î∞ýº∂°¢—ß–£µ»∑Ω√ʵƒπÿœµ£¨±ÿ–Î∞¥≥…º®‘Ÿ¥”’‚10000»À÷–”√∑÷≤„≥È—˘∑Ω∑®≥È≥ˆ20»À◊˜Ω¯“ª≤Ω∑÷Œˆ£¨‘Ú≥…º®‘⁄![]() µƒ’‚∂Œ”¶≥È∂ý…Ÿ»À£ø
µƒ’‚∂Œ”¶≥È∂ý…Ÿ»À£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
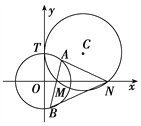
°æƒø°ø»ÁÕº£¨“—÷™‘≤C”Îy÷·œý«–”⁄µ„T(0,2)£¨”Îx÷·µƒ’˝∞Î÷·Ωª”⁄¡Ωµ„![]() (µ„
(µ„![]() ‘⁄µ„
‘⁄µ„![]() µƒ◊Û≤ý)£¨«“
µƒ◊Û≤ý)£¨«“![]() .
.
(1)«Û‘≤Cµƒ∑Ω≥ãª(2)π˝µ„![]() »Œ◊˜“ª÷±œþ”Α≤O£∫
»Œ◊˜“ª÷±œþ”Α≤O£∫ ![]() œýΩª”⁄
œýΩª”⁄![]() ¡Ωµ„£¨¡¨Ω”
¡Ωµ„£¨¡¨Ω”![]() £¨«Û÷§£∫
£¨«Û÷§£∫ ![]() ∂®÷µ£Æ
∂®÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø4‘¬23»’ «°∞ ¿ΩÁ∂¡ È»’°±,ƒ≥÷–—ß‘⁄¥À∆⁄º‰ø™’π¡À“ªœµ¡–µƒ∂¡ ÈΩÔ˝ªÓ∂Ø,Œ™¡ÀΩ‚±æ–£—ß…˙øŒÕ‚‘ƒ∂¡«Èøˆ,—ß–£Àʪ˙≥È»°¡À100√˚—ß…˙∂‘∆‰øŒÕ‚‘ƒ∂¡ ±º‰Ω¯––µ˜≤È,œ¬√Ê «∏˘æðµ˜≤ÈΩ·π˚ªÊ÷∆µƒ—ß…˙»’æ˘øŒÕ‚‘ƒ∂¡ ±º‰(µ•Œª:min)µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº,»ÙΩ´»’æ˘øŒÕ‚‘ƒ∂¡ ±º‰≤ªµÕ”⁄60 minµƒ—ß…˙≥∆Œ™°∞ È≥Ê°±,µÕ”⁄60 minµƒ—ß…˙≥∆Œ™°∞¿¡≥Ê°±,

(1)«Ûxµƒ÷µ≤¢π¿º∆»´–£3 000√˚—ß…˙÷–°∞ È≥Ê°±¥Û∏≈”–∂ý…Ÿ√˚—ß…˙?(Ω´∆µ¬ ”Œ™∏≈¬ )
(2)∏˘æð“—÷™Ãıº˛ÕÍ≥…œ¬√Ê2°¡2µƒ¡–¡™±Ì,≤¢≈–∂œƒÐ∑Ò‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝0.01µƒ«∞÷œ¬»œŒ™°∞ È≥Ê°±”Ζ‘±”–πÿ:

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫Ø ˝f£®x£©µƒ∂®“”ڌ™[©Å1£¨1]£¨ÕºœÛ»ÁÕº1À˘ 棪∫Ø ˝g£®x£©µƒ∂®“”ڌ™[©Å2£¨2]£¨ÕºœÛ»ÁÕº2À˘ 棨…Ë∫Ø ˝f£®g£®x£©£©”–m∏ˆ¡„µ„£¨∫Ø ˝g£®f£®x£©£©”–n∏ˆ¡„µ„£¨‘Úm+nµ»”⁄£®°°°°£©

A. 6 B. 10 C. 8 D. 1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚ƒ≥µÿ«¯ƒ≥÷÷≈©≤˙∆∑µƒƒÍ≤˙¡ø![]() £®µ•Œª£∫∂÷£©∂‘º€∏Ò
£®µ•Œª£∫∂÷£©∂‘º€∏Ò![]() £®µ•Œª£∫«ß‘™/∂÷£©∫Õ¿˚»Û
£®µ•Œª£∫«ß‘™/∂÷£©∫Õ¿˚»Û![]() µƒ”∞œÏ£¨∂‘Ω¸ŒÂƒÍ∏√≈©≤˙∆∑µƒƒÍ≤˙¡ø∫Õº€∏ÒÕ≥º∆»Áœ¬±Ì£∫
µƒ”∞œÏ£¨∂‘Ω¸ŒÂƒÍ∏√≈©≤˙∆∑µƒƒÍ≤˙¡ø∫Õº€∏ÒÕ≥º∆»Áœ¬±Ì£∫
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
“—÷™![]() ∫Õ
∫Õ![]() æþ”–œþ–‘œýπÿπÿœµ.
æþ”–œþ–‘œýπÿπÿœµ.
£®¢Ò£©«Û![]() πÿ”⁄
πÿ”⁄![]() µƒœþ–‘ªÿπÈ∑Ω≥Ã
µƒœþ–‘ªÿπÈ∑Ω≥Ã![]() £ª
£ª
£®¢Ú£©»Ù√ø∂÷∏√≈©≤˙∆∑µƒ≥…±æŒ™2«ß‘™£¨ºŸ…Ë∏√≈©≤˙∆∑ø…»´≤ø¬Ù≥ˆ£¨‘§≤‚µ±ƒÍ≤˙¡øŒ™∂ý…Ÿ∂÷ ±£¨ƒÍ¿˚»Û![]() »°µΩ◊Ó¥Û÷µ£ø£®±£¡Ù“ªŒª–° ˝£©
»°µΩ◊Ó¥Û÷µ£ø£®±£¡Ù“ªŒª–° ˝£©
≤Œøº ˝æðº∞π´ Ω£∫ ![]() £¨
£¨ ![]() £¨
£¨

 £¨
£¨ ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄º∏∫ŒÃÂ÷–£¨Àƒ±þ–Œ![]() Œ™¡‚–Œ£¨∂‘Ω«œþ
Œ™¡‚–Œ£¨∂‘Ω«œþ![]() ”Î
”Î![]() µƒΩªµ„Œ™
µƒΩªµ„Œ™![]() £¨Àƒ±þ–Œ
£¨Àƒ±þ–Œ![]() Œ™Ã𖌣¨
Œ™Ã𖌣¨ ![]() .
.

£®¢Ò£©»Ù![]() £¨«Û÷§£∫
£¨«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®¢Ú£©«Û÷§£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®¢Û£©»Ù![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨«Û
£¨«Û![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«.
À˘≥…Ω«.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™πÿ”⁄![]() µƒ“ª‘™∂˛¥Œ∑Ω≥Ã
µƒ“ª‘™∂˛¥Œ∑Ω≥Ã![]() £¨∆‰÷–
£¨∆‰÷–![]() °£
°£
£®I£©»Ù![]() Àʪ˙—°◊‘ºØ∫œ
Àʪ˙—°◊‘ºØ∫œ![]() £¨
£¨![]() Àʪ˙—°◊‘ºØ∫œ
Àʪ˙—°◊‘ºØ∫œ![]() £¨«Û∑Ω≥Ô– µ∏˘µƒ∏≈¬ ;
£¨«Û∑Ω≥Ô– µ∏˘µƒ∏≈¬ ;
£®¢Ú£©»Ù![]() Àʪ˙—°◊‘«¯º‰
Àʪ˙—°◊‘«¯º‰![]() £¨
£¨![]() Àʪ˙—°◊‘«¯º‰
Àʪ˙—°◊‘«¯º‰![]() £¨«Û∑Ω≥Ô– µ∏˘µƒ∏≈¬ °£
£¨«Û∑Ω≥Ô– µ∏˘µƒ∏≈¬ °£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com