
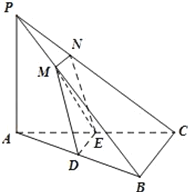
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() .D,E分别为
.D,E分别为![]() ,
,![]() 的中点,过
的中点,过![]() 的平面与
的平面与![]() ,
,![]() 相交于点M,N(M与P,B不重合,N与P,C不重合).
相交于点M,N(M与P,B不重合,N与P,C不重合).
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)若直线![]() 与直线
与直线![]() 所成角的余弦值
所成角的余弦值![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)![]() 为
为![]() 的中位线,从而得到
的中位线,从而得到![]() ,然后根据线面平行的判定定理及性质定理即可得到
,然后根据线面平行的判定定理及性质定理即可得到![]() ,从而
,从而![]() ,即
,即![]() ;
;
(2)过B作![]() ,容易说明
,容易说明![]() ,
,![]() ,
,![]() 三条直线互相垂直,从而以B为原点,
三条直线互相垂直,从而以B为原点,![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立空间直角坐标系,这样即可求得
所在直线为x,y,z轴建立空间直角坐标系,这样即可求得![]() ,
,![]() ,
,![]() 的坐标.从而可求出平面
的坐标.从而可求出平面![]() 的一个法向量坐标
的一个法向量坐标![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,根据
,根据![]() 即可求出
即可求出![]() ;
;
(3)根据图形设![]() ,由M点在棱
,由M点在棱![]() 上,便可得到
上,便可得到![]() ,从而表示M为
,从而表示M为![]() ,根据直线
,根据直线![]() 与直线
与直线![]() 所成角的余弦值
所成角的余弦值![]() ,设直线
,设直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,从而通过
,从而通过 即可求出
即可求出![]() ,从而求出M点坐标,由两点间距离公式即可求出
,从而求出M点坐标,由两点间距离公式即可求出![]() .
.
(1)证明:∵D,E分别为![]() ,
,![]() 的中点;
的中点;
∴![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
∴![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ;
;
∴![]() ;
;
∴![]() ;
;
(2)如图,在平面![]() 内作
内作![]() ,则根据:
,则根据:

![]() 底面
底面![]() ,及
,及![]() 即知,
即知,![]() ,
,![]() ,
,![]() 两两垂直;
两两垂直;
∴以B为坐标原点,![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立如图所示空间直角坐标系,则:
所在直线为x,y,z轴建立如图所示空间直角坐标系,则:
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
∴![]() ,
,![]() ,
,![]() ,;
,;
设平面![]() 的法向量为
的法向量为![]() ;
;
则由 得:
得:
 ,令
,令![]() ,得
,得![]() ,
,![]() ;
;
∴![]() ;
;
设直线![]() 和平面
和平面![]() 所成角为
所成角为![]() ,则:
,则:
 ;
;
又![]() ;
;
∴![]() ;
;
即直线![]() 和平面
和平面![]() 所成角为
所成角为![]() ;
;
(3)设![]() ,M在棱
,M在棱![]() 上,则:
上,则:![]() ,(
,(![]() );
);
∴![]() ;
;
∴![]() ,
,![]() ;
;
∴![]() ,
,![]() ;
;
因为直线![]() 与直线
与直线![]() 所成角的余弦值
所成角的余弦值![]() ;
;
设直线![]() 和直线
和直线![]() 所成角为
所成角为![]() ;
;
所以 ;
;
∴![]() ;
;
解得![]() ,或
,或![]() (舍去);
(舍去);
∴![]() ;
;
∴![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为数列
为数列![]() 的前n项和, 且满足
的前n项和, 且满足![]() 为常数
为常数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)是否存在实数 ![]() ,使得数列
,使得数列![]() 为等差数列?若存在,求出
为等差数列?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)当![]() 时,若数列
时,若数列![]() 满足
满足![]() ,且
,且![]() ,令
,令![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线
,它的一个焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线过点
的直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,设点
两点,设点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过点
过点![]()
![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 的纵截距为
的纵截距为![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,在同一个坐标系中,
,在同一个坐标系中,![]() 及
及![]() 的部分图象如图所示,则( ).
的部分图象如图所示,则( ).

A. 当![]() 时,
时,![]() 取得最大值 B. 当
取得最大值 B. 当![]() 时,
时,![]() 取得最大值
取得最大值
C. 当![]() 时,
时,![]() 取得最小值 D. 当
取得最小值 D. 当![]() 时,
时,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
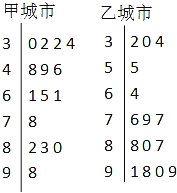
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10日,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为3,中位数为4;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,总体方差为3;
丁地:中位数为2,众数为3;
则甲、乙、两、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com