
【题目】正整数数列![]() 满足:
满足:![]() ,
,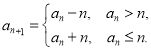
(1)写出数列![]() 的前5项;
的前5项;
(2)将数列![]() 中所有值为1的项的项数按从小到大的顺序依次排列,得到数列
中所有值为1的项的项数按从小到大的顺序依次排列,得到数列![]() ,试用
,试用![]() 表示
表示![]() (不必证明);
(不必证明);
(3)求最小的正整数![]() ,使
,使![]() .
.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,准线方程为
,准线方程为![]() ,直线
,直线![]() 过定点
过定点![]() (
(![]() )且与抛物线交于
)且与抛物线交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求抛物线的方程;
(2)![]() 是否为定值,若是,求出这个定值;若不是,请说明理由;
是否为定值,若是,求出这个定值;若不是,请说明理由;
(3)当![]() 时,设
时,设![]() ,记
,记![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
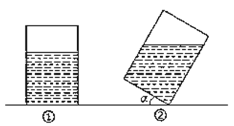
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的
年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的![]() 抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后
抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后![]() 分钟,瓶内液面与进气管的距离为
分钟,瓶内液面与进气管的距离为![]() 厘米,已知当
厘米,已知当![]() 时,
时,![]() .如果瓶内的药液恰好
.如果瓶内的药液恰好![]() 分钟滴完.则函数
分钟滴完.则函数![]() 的图像为( )
的图像为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,如图2,点
折起,如图2,点![]() 是棱
是棱![]() 上的点.
上的点.
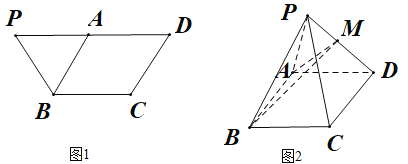
(1)若![]() 为
为![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试确定
,试确定![]() 的位置,使二面角
的位置,使二面角![]() 的余弦值等于
的余弦值等于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com