
已知椭圆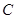 的中心为直角坐标系
的中心为直角坐标系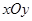 的原点,焦点在
的原点,焦点在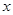 轴上,它的一个顶点到两个焦点的距离分别是7和1
轴上,它的一个顶点到两个焦点的距离分别是7和1
(1)求椭圆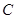 的方程
的方程
(2)若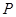 为椭圆
为椭圆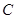 的动点,
的动点,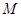 为过
为过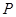 且垂直于
且垂直于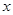 轴的直线上的点,
轴的直线上的点,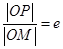 (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点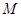 的轨迹方程,并说明轨迹是什么曲线?
的轨迹方程,并说明轨迹是什么曲线?
(1)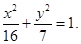 (2)轨迹方程为
(2)轨迹方程为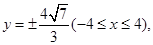 轨迹是两条平行于x轴的线段.
轨迹是两条平行于x轴的线段.
【解析】
试题分析:(1)设椭圆长半轴长及分别为a,c,由已知得
{ 解得a=4,c=3,
解得a=4,c=3,
所以椭圆C的方程为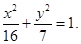
(2)设M(x,y),P(x, ),其中
),其中 由已知得
由已知得
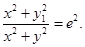
而 ,故
,故 ①
①
由点P在椭圆C上得

代入①式并化简得
所以点M的轨迹方程为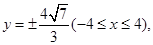 轨迹是两条平行于x轴的线段.
轨迹是两条平行于x轴的线段.
考点:椭圆的标准方程;椭圆的简单性质;轨迹方程的求法。
点评:求轨迹方程的基本步骤:①建立适当的平面直角坐标系,设P(x,y)是轨迹上的任意一点;②寻找动点P(x,y)所满足的条件;③用坐标(x,y)表示条件,列出方程f(x,y)=0;④化简方程f(x,y)=0为最简形式;⑤证明所得方程即为所求的轨迹方程,注意验证。


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个顶点到两个
轴上,它的一个顶点到两个
焦点的距离分别是7和1
(1)求椭圆![]() 的方程‘
的方程‘
(2)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个项点到两个焦点的距离分别是7和1
轴上,它的一个项点到两个焦点的距离分别是7和1
(1)求椭圆![]() 的方程‘
的方程‘
(2)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]()
(e为椭圆C的离心率),求点![]() 的轨迹方程,并说明轨迹是什么曲线。
的轨迹方程,并说明轨迹是什么曲线。
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个项点到两个焦点的距离分别是7和1.
轴上,它的一个项点到两个焦点的距离分别是7和1.
(I)求椭圆![]() 的方程;
的方程;
(II)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]() (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点![]() 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2015届河北衡水中学高二上第四次调研考试文数学卷(解析版) 题型:解答题
已知椭圆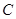 的中心为直角坐标系
的中心为直角坐标系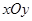 的原点,焦点在
的原点,焦点在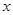 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆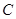 的方程;
的方程;
(2)若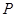 为椭圆
为椭圆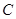 的动点,
的动点,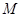 为过
为过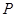 且垂直于
且垂直于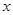 轴的直线上的点,
轴的直线上的点,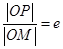 (
(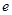 为椭圆的离心率),求点
为椭圆的离心率),求点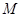 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com