
(13分)(2011•广东)如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的,A,A′,B,B′分别为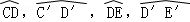 的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
(1)证明:O1′,A′,O2,B四点共面;
(2)设G为A A′中点,延长A′O1′到H′,使得O1′H′=A′O1′.证明:BO2′⊥平面H′B′G
(1)(2)见解析
解析试题分析:(1)要证O1′,A′,O2,B四点共面,即可证四边形BO2A′O1′为平面图形,根据A′O1′与B′O2′在未平移时属于同一条直径
知道A′O1′∥B′O2′即BO2∥A′O1′再根据BO2=A′O1′=1即可得到四边形BO2A′O1′是平行四边形,则证.
(2)建立空间直角坐标系,要证BO2′⊥平面H′B′G只需证 ,
, ,根据坐标运算算出
,根据坐标运算算出 •
• ,
,
 的值均为0即可
的值均为0即可
证明:(1)∵B′,B分别是中点
∴BO2∥B′O2′
∵A′O1′与B′O2′在未平移时属于同一条直径
∴A′O1′∥B′O2′
∴BO2∥A′O1′
∵BO2=A′O1′=1
∴四边形BO2A′O1′是平行四边形
即O1′,A′,O2,B四点共面
(2)以D为原点,以向量DE所在的直线为X轴,以向量DD′所在的直线为Z轴,建立如图空间直角坐标系,
则B(1,1,0),O2′(0,1,2),H′(1,﹣1,2),A(﹣1,﹣1,0),G(﹣1,﹣1,1),B′(1,1,2)
则 =(﹣1,0,2),
=(﹣1,0,2), =(﹣2,﹣2,﹣1),
=(﹣2,﹣2,﹣1), =(0,﹣2,0)
=(0,﹣2,0)
∵ •
• =0,
=0,
 =0
=0
∴BO2′⊥B′G,BO2′⊥B′H′
即 ,
,
∵B′H′∩B′G=B′,B′H′、B′G?面H′GB′
∴BO2′⊥平面H′B′G
点评:本题考查了直线与平面垂直的判定,棱柱的结构特征,平面的基本性质及推论以及空间向量的基本知识,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面
为正方形, ,
, ,
, 分别是
分别是 ,
, 的 中点.
的 中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)若 是线段
是线段 上一动点,试确定
上一动点,试确定 点位置,
点位置,
使 平面
平面 ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积.(锥体体积公式V= Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C到平面A1BD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4, ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC 平面
平面 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且 平面
平面 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2012•广东)如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com