
| A. | 该函数值域为[-1,1] | |
| B. | 当且仅当x=2kπ+$\frac{π}{2}$(k∈Z)时,函数取最大值1 | |
| C. | 该函数是以π为最小正周期的周期函数 | |
| D. | 当π+2kπ<x<2kπ+$\frac{3π}{2}$(k∈Z)时,f(x)<0 |
分析 分别画出y=sinx和y=cosx的图象,取上方的图象,可得f(x)的图象,通过图象观察可得最值,即可判断A;由最高点,即可判断B;由周期为2π,可判断C;由f(x)<0的解,即可判断D.
解答 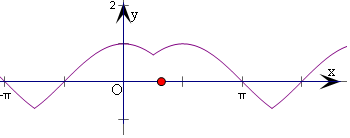 解:分别画出y=sinx和y=cosx的图象,
解:分别画出y=sinx和y=cosx的图象,
取上方的图象,可得如图:
即有f(x)的最大值为1,最小值为-$\frac{\sqrt{2}}{2}$,故A错;
当x=2kπ+$\frac{π}{2}$(k∈Z)或x=2kπ(k∈Z时,函数取最大值1,故B错;
函数的最小正周期为$\frac{5π}{4}$-(-$\frac{3π}{4}$)=2π,故C错;
由图象可得当π+2kπ<x<2kπ+$\frac{3π}{2}$(k∈Z)时,f(x)<0,故D正确.
故选:D.
点评 本题考查分段函数的图象和应用,考查正弦函数、余弦函数的图象和性质,注意数形结合思想的运用,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | -3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
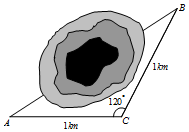 如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )
如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )| A. | $\sqrt{3}$km | B. | $\sqrt{2}$km | C. | 1.5km | D. | 2km |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-∞,-1)或(3,+∞) | C. | (-3,1) | D. | (-∞,-3)或(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com